线性回归(正规方程求解,损失函数形式为最小二乘法)
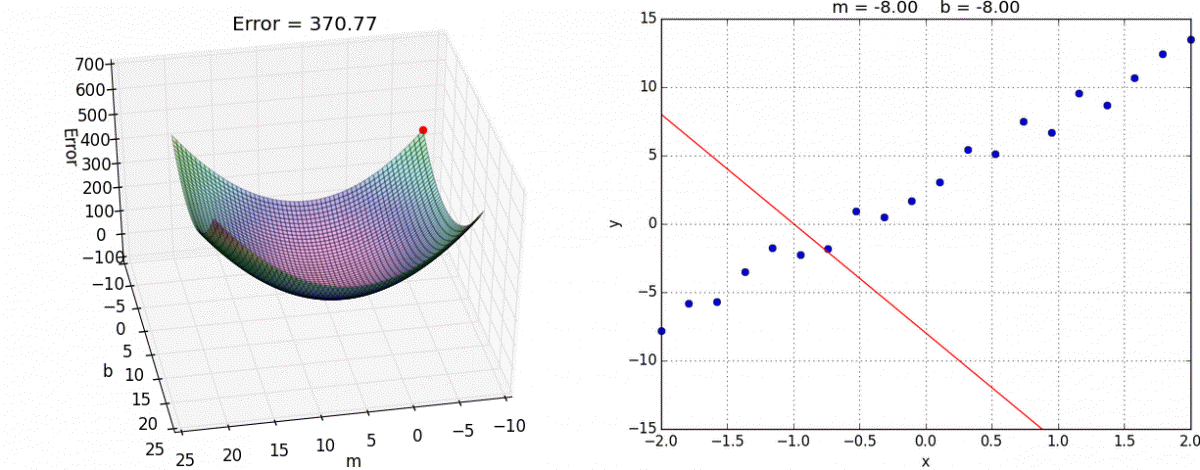
案例:
from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error import joblib def linear1(): """ 正规方程的优化方法对波士顿房价进行预测 :return: """ # 1)获取数据 boston = load_boston() # 2)划分数据集 x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22) # 3)标准化 transfer = StandardScaler() x_train = transfer.fit_transform(x_train) x_test = transfer.transform(x_test) # 4)预估器 estimator = LinearRegression() estimator.fit(x_train, y_train) # 5)得出模型 print("正规方程-权重系数为:\n", estimator.coef_) print("正规方程-偏置为:\n", estimator.intercept_) # 6)模型评估 y_predict = estimator.predict(x_test) print("预测房价:\n", y_predict) error = mean_squared_error(y_test, y_predict) print("正规方程-均方误差为:\n", error) return None
梯度下降
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高O(n3) |
欠拟合
学习到数据的特征过少
解决:
增加数据的特征数量
过拟合
原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决:
正则化
L1
损失函数 + λ惩罚项
LASSO
L2 更常用
损失函数 + λ惩罚项
Ridge - 岭回归
案例:
1.梯度下降
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
def linear2(): """ 梯度下降的优化方法对波士顿房价进行预测 :return: """ # 1)获取数据 boston = load_boston() print("特征数量:\n", boston.data.shape) # 2)划分数据集 x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22) # 3)标准化 transfer = StandardScaler() x_train = transfer.fit_transform(x_train) x_test = transfer.transform(x_test) # 4)预估器 estimator = SGDRegressor(learning_rate="constant", eta0=0.01, max_iter=10000, penalty="l2") estimator.fit(x_train, y_train) # 5)得出模型 print("梯度下降-权重系数为:\n", estimator.coef_) print("梯度下降-偏置为:\n", estimator.intercept_) # 6)模型评估 y_predict = estimator.predict(x_test) print("预测房价:\n", y_predict) error = mean_squared_error(y_test, y_predict) print("梯度下降-均方误差为:\n", error) return None
2.岭回归(加L2正则项的线性回归)
def linear3(): """ 岭回归对波士顿房价进行预测 :return: """ # 1)获取数据 boston = load_boston() print("特征数量:\n", boston.data.shape) # 2)划分数据集 x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22) # 3)标准化 transfer = StandardScaler() x_train = transfer.fit_transform(x_train) x_test = transfer.transform(x_test) # 4)预估器 estimator = Ridge(alpha=0.5, max_iter=10000) estimator.fit(x_train, y_train) # 保存模型 joblib.dump(estimator, "my_ridge.pkl") # 加载模型 estimator = joblib.load("my_ridge.pkl") # 5)得出模型 print("岭回归-权重系数为:\n", estimator.coef_) print("岭回归-偏置为:\n", estimator.intercept_) # 6)模型评估 y_predict = estimator.predict(x_test) print("预测房价:\n", y_predict) error = mean_squared_error(y_test, y_predict) print("岭回归-均方误差为:\n", error) return None
原文:https://www.cnblogs.com/sima-3/p/14813627.html