MLP的BP算法

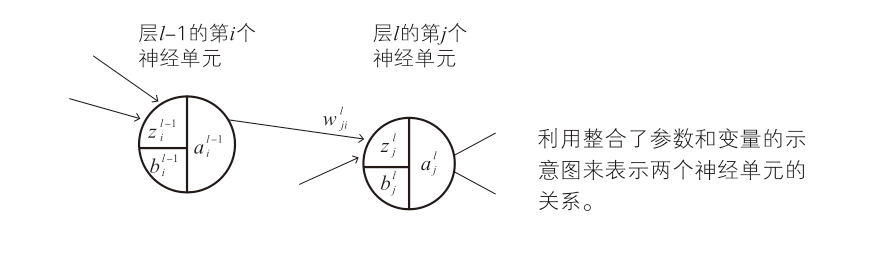
1. 计算输出层的加权和输入 \(z^L\) 的梯度

   1. 元素形式

      \[\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma‘(z^L_j) \end{eqnarray} \]

   2. 矩阵形式

      \[\begin{eqnarray} \delta^L = \nabla_a C \odot \sigma‘(z^L) \end{eqnarray} \]

      或

      \[\begin{eqnarray} \delta^L = \nabla_a C\cdot\Sigma‘(z^L) \end{eqnarray} \]

2. 递归地计算前面层的加权和输入 \(z^l\) 的梯度

   1. 元素形式

      \[\begin{eqnarray} \delta_k^l=\sum_j\delta_j^{l+1}\cdot w_{jk}^{l+1}\cdot\sigma‘(z_k^l) \end{eqnarray} \]

   2. 矩阵形式

      \[\begin{eqnarray} \delta^l=(\delta^{l+1}\cdot w^{l+1})\odot\sigma‘(z^l) \end{eqnarray} \]

3. 计算偏置 \(b^l\) 的梯度

   1. 元素形式

      \[\begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \frac{\partial C}{\partial z_j^l}\cdot\frac{\partial z_j^l}{\partial b_j^l}=\delta_j^l \end{eqnarray} \]

   2. 矩阵形式

      \[\begin{eqnarray} \frac{\partial C}{\partial b^l}=\frac{\partial C}{\partial z^l}\frac{\partial z^l}{\partial b^l}=\frac{\partial C}{\partial z^l}=\delta^l \end{eqnarray} \]

4. 计算权重 \(w^l\) 的梯度

   1. 元素形式

      \[\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = \delta^l_ja^{l-1}_k \end{eqnarray} \]

   2. 矩阵形式

      \[\begin{eqnarray} \frac{\partial C}{\partial w} = \delta^l\otimes a^{l-1} \end{eqnarray} \]

.

MLP的BP算法

原文：https://www.cnblogs.com/cookcooller/p/14815583.html