1 前言

　　机器学习和深度学习里面都至关重要的一个环节就是优化损失函数，一个模型只有损失函数收敛到一定的值，才有可能会有好的结果，降低损失的工作就是优化方法需做的事。常用的优化方法：梯度下降法家族、牛顿法、拟牛顿法、共轭梯度法、Momentum、Nesterov Momentum、Adagrad、RMSprop、Adam等。

　　梯度下降法不论是在线性回归还是Logistic回归中，主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。

2 梯度下降算法

2.1 场景假设

　　梯度下降法的基本思想可以类比为一个下山的过程。
　　假设这样一个场景：一个人被困在山上，需要从山上找到山的最低点。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。

　　怎么做呢？首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处。

2.2 梯度下降

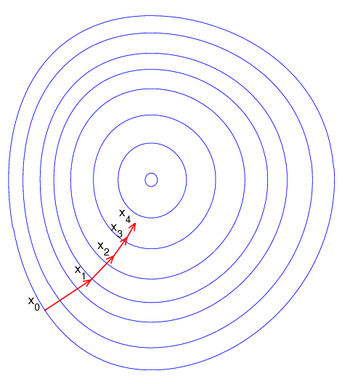
　　梯度下降的基本过程就和下山的场景很类似。

　　首先，我们有一个可微分的函数，代表着一座山。目标是找到这个函数的最小值，也就是山底。

　　根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走。对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！

　　重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。

2.2.1 微分

　　微分例子：

　　1.单变量的微分，函数只有一个变量时

　　　　$\frac{\mathrm{d}(x^{2}) }{\mathrm{d} x} =2x$

　　2.多变量的微分，当函数有多个变量的时候，分别对每个变量进行求微分

　　　　$\frac{\partial (x^{2}y^{2})}{\partial x} =2xy^{2}$

2.2.2 梯度

　　梯度实际上就是多变量微分的一般化。

　　例子：

　　　　$J(\theta )=5-(4\theta_{1} +3\theta_{2}-2\theta_{3})$

　　可以看到，梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用$<>$包括起来，说明梯度其实一个向量。

• 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率。
• 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向。

2.2.3 数学解释

　　数学公式：$\theta ^{1} =\theta ^{0} +\alpha \bigtriangledown J(\theta)$

　　意义是：J是关于$\theta$的一个函数，当前所处位置为$\theta ^{0}$点，要从这个点走到 J 的最小值点。首先先确定前进的方向：梯度的反向。然后走一段距离的步长：$\alpha$，走完这个段步长，到达$\theta ^{1}$！

2.2.4 学习率α

　　$\alpha$在梯度下降算法中被称为学习率或者步长。通过$\alpha$来控制每一步距离，以保证步子不要跨太大，避免走太快，错过最低点。同时也要保证不要走的太慢，影响效率。$\alpha$不能太大也不能太小，太小的话，可能导致走不到最低点；太大的话，导致错过最低点。

2.2.5 梯度乘负号

　　梯度前加负号，意味着朝梯度相反方向前进。梯度的方向就是函数在此点上升最快的方向。梯度下降需要朝下降最快的方向前进，自然是负梯度的方向，所以需要加上负号。

3 实例

3.1 单变量函数的梯度下降

　　假设有一个单变量函数：$J(\theta) =\theta ^{2} $

　　函数的微分：$J^{‘} (\theta) =2\theta$

　　初始化：设置初始位置$ \theta^{0}=1$

　　设置学习率：$\alpha =0.4$

　　根据梯度下降的计算公式：$\theta ^{1} =\theta ^{0} +\alpha \bigtriangledown J(\theta)$

　　计算过程：

　　$\theta ^{0} =1$

　　$\theta ^{1} =\theta ^{0}-\alpha J ^{‘}(\theta ^{0})=1-0.4*2=0.2$

　　$\theta ^{2} =\theta ^{1}-\alpha J ^{‘}(\theta ^{1})=0.2-0.4*0.4=0.04$

　　$\theta ^{3} =0.08$

　　$\theta ^{4} =0.0016$

　　如图，经过四次的运算，也就是走了四步，基本抵达函数最低点，也就是山底。

3.2 多变量函数的梯度下降

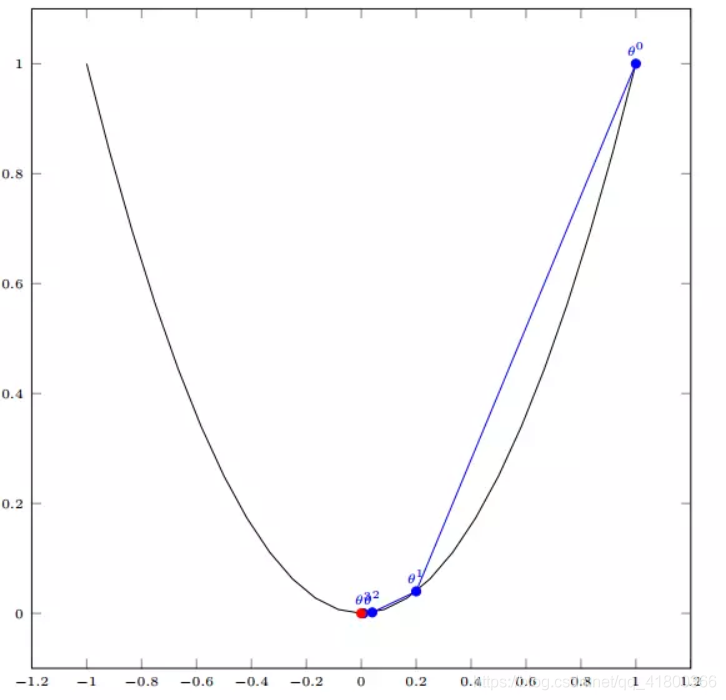
　　假设有一个目标函数：$J(\theta)=\theta_{1}^{2} +\theta_{2}^{2}$

　　假设初始起点：$\theta^{0}= (1,3)$

　　初始学习率：$\alpha =0.1$

　　函数的梯度为：$\bigtriangledown J(\theta)=<2\theta_{1},2\theta_{2}>$

　　计算过程：

　　$\theta^{0} =(1,3)$

　　$\theta^{1} =\theta^{0}-\alpha \bigtriangledown J(\theta)=(1,3)-0.1*(2,6)=(0.8,2.4)$

　　$\theta^{2} =\theta^{1}-\alpha \bigtriangledown J(\theta)=(0.8,2.4)-0.1*(1.6,4.8)=(0.64,1.92)$

　　$.....$

　　我们发现，已经基本靠近函数的最小值点：

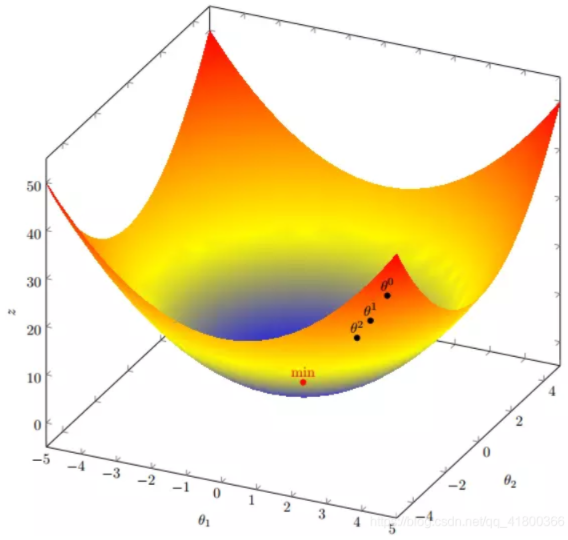
参考文献：

梯度下降算法原理讲解——机器学习

机器学习——梯度下降法

原文：https://www.cnblogs.com/BlairGrowing/p/14819885.html