题面分析

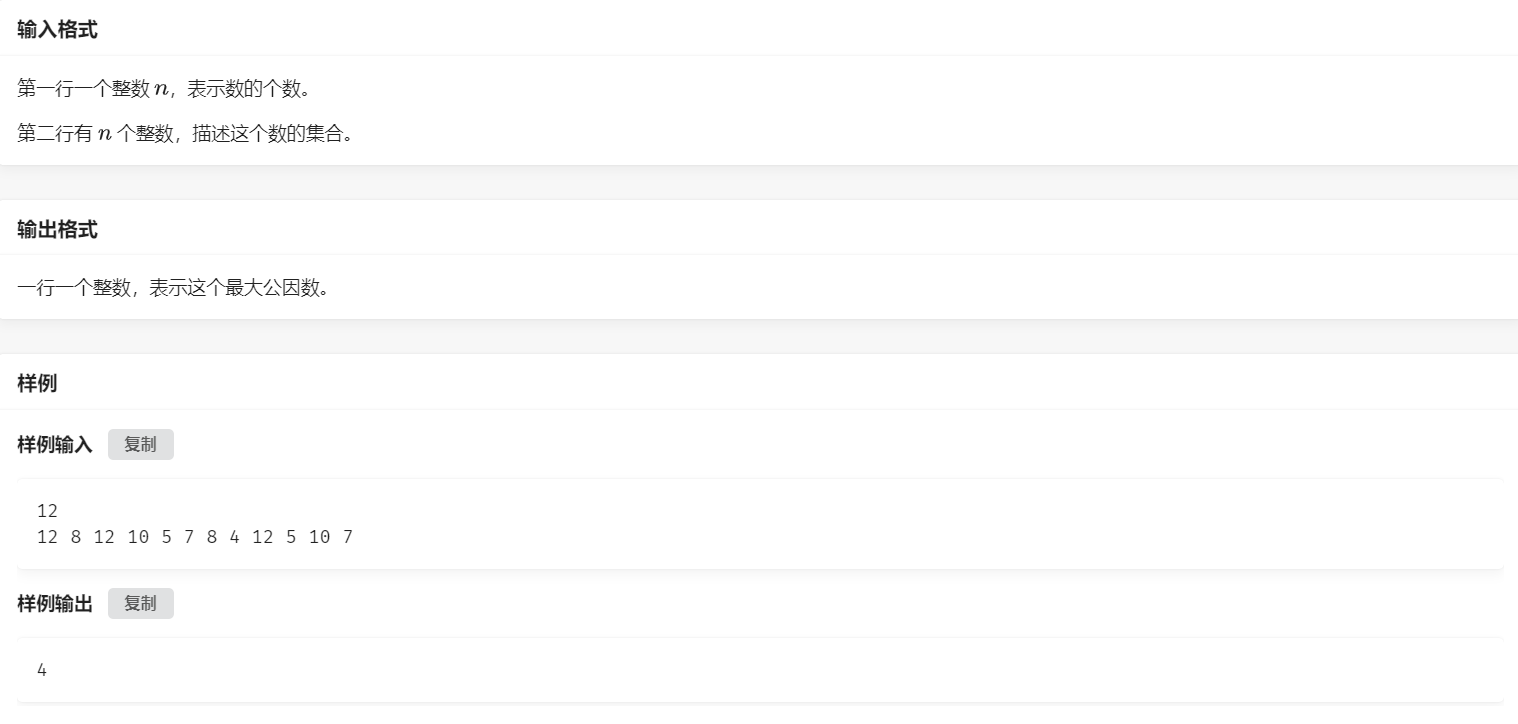
给定 \(n\) 个数，请选出至少一半的数，使得它们的最大公因数最大。
求出它们的最大公因数。

算法分析

我们可以枚举一下这个最大公因数，因为每个 \(a_i\) 的数据并不是很大（\(1\le a_i \le 3000\)），所以最大公因数只有可能在这个范围内。
那么可以从 \(1\) 到 \(3000\) 进行枚举最大公因数，看看能不能被 \(a_i\) 整除，把能被整除个数记下来。
然后对每个枚举的最大公因数能被 \(a_i\) 整除个数大于 \(n\) 的一半的，取一个最大值就是答案了。
显然，这是一道暴力枚举。

复杂度分析

\(O(3000*n)\)

AC代码

#include<iostream>
#include<cstdio>
using namespace std;
int n,ans;
int a[3005],sum[3005];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<=3000;i++){
		for(int j=1;j<=n;j++){
			if(a[j]%i==0) sum[i]++;//计算这个数能被a[i]整除的个数
		}
	}
	for(int i=1;i<=3000;i++) if(sum[i]>=n/2) ans = max(ans,i);//对符合题意的最大公因数去最大值
	printf("%d",ans);
	return 0;
}

FYMS-OI #5062. YAOI Round #9 (Div.2) B. I love you 题解

原文：https://www.cnblogs.com/youlinaixuan/p/14823871.html