给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
输入:
[[0,0,0],
[0,1,0],
[0,0,0]]
输出:
[[0,0,0],
[0,1,0],
[0,0,0]]
示例 2:
输入:
[[0,0,0],
[0,1,0],
[1,1,1]]
输出:
[[0,0,0],
[0,1,0],
[1,2,1]]
提示:
给定矩阵的元素个数不超过 10000。
给定矩阵中至少有一个元素是 0。
矩阵中的元素只在四个方向上相邻: 上、下、左、右。
超级暴力解法:(i为行,j为列)
对于矩阵中的每个元素,如果它的值为0,那么离它最近的0就是它自己。如果它的值为1,那么我们就需要找出离他最近的0,并且返回这个距离值。
向上遍历的规则为:i-1&&i-1>=0
向下遍历的规则为:i+1&&i+1<row
向左遍历规则为:j-1&&j-1>=0
向右遍历规则为:j+1&&j+1<col
并且一个方向上如果没有遇到0就距离去除
func updateMatrix(mat [][]int) [][]int {
log.Println("===========================")
if len(mat)==0{
return nil
}
row := len(mat)
col := len(mat[0])
result := make([][]int,row)
for i:=0;i<row;i++{
result[i] = make([]int,col)
}
for i:=0;i<row;i++{
for j:=0;j<col;j++{
if mat[i][j] == 0{
continue
}
tmp := make([]int,0)
if above, isZero := getDistanceAbove(mat,row,col,i,j); isZero {
tmp = append(tmp,above)
}
if down, isZero := getDistanceDown(mat,row,col,i,j); isZero {
tmp = append(tmp,down)
}
if left, isZero := getDistanceLeft(mat,row,col,i,j); isZero {
tmp = append(tmp,left)
}
if right, isZero := getDistanceRight(mat,row,col,i,j); isZero {
tmp = append(tmp,right)
}
if len(tmp)==0{
result[i][j] = 0
}else{
result[i][j] = getMin(tmp)
}
}
}
for i:=0;i<len(result);i++{
log.Println(result[i])
}
return result
}
// getDistanceAbove 遍历上面获取到最近的距离
func getDistanceAbove(mat [][]int,row int,col int,i int,j int)(int,bool){
result := 0
for a:=i-1;a>=0;a--{
if mat[a][j]!=0{
result++
}else{
return result+1,true
}
if a==0{
return result,false
}
}
return result,false
}
// getDistanceDown 遍历下面获取到最近的距离
func getDistanceDown(mat [][]int,row int,col int,i int,j int)(int,bool){
result := 0
for a:=i+1;a<row;a++{
if mat[a][j]!=0{
result++
}else{
//log.Println(result+1)
return result+1,true
}
if a==row-1{
return result,false
}
}
return result,false
}
// getDistanceLeft 遍历左边获取到最近的距离
func getDistanceLeft(mat [][]int,row int,col int,i int,j int)(int,bool){
result := 0
for a:=j-1;a>=0;a--{
if mat[i][a]!=0{
result++
}else{
//log.Println(result+1)
return result+1,true
}
if a==0{
return result,false
}
}
return result,false
}
// getDistanceRight 遍历右边获取最近的距离
func getDistanceRight(mat [][]int,row int,col int,i int,j int)(int,bool){
result := 0
for a:=j+1;a<col;a++{
if mat[i][a]!=0{
result++
}else{
//log.Println(result+1)
return result+1,true
}
if a==col-1{
return result,false
}
}
return result,false
}
结果:题目理解失误,认为只有上下左右上遇到0的才是距离,但是可以转弯的。
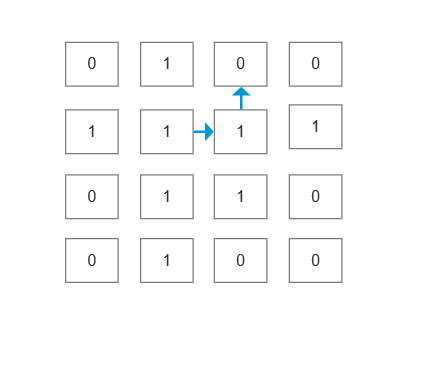
从0的位置开始进行广度优先搜索。广度优先搜索可以找到从起点到其余所有点的最短距离,因此如果我们从0开始搜索,每次搜索到一个1,就可以得到0到这个1的最短距离,也就是离这个1最近的0的距离,这个是对于只有一个0的情况下的,如果有多个0的话,就将这些0的位置都加入到队列中,分别进行广度优先算法。
单元广度优先:对于树的广度优先算法是把root节点入队,再一层一层无脑遍历就行。
多元广度优先:将多个源放在队列中后,再一个一个取出来做广度优先。但是这样做需要注意注意:对于树是有向的因此不需要标尺是否访问过,而对于无向图来说,必须得标志是否访问过,并且为了防止某个节点多次入队,需要再其入队之前就将其设置为已访问。
做法:在这里0就是源,将矩阵中所有的0的位置入队,并且将1的位置设置为-1(表示没有访问过)。设置每个源的上下左右的位置,用于方便计算放到数组中,/[]/[]int{{0,-1},{0,1},{-1,0},{1,0}}。然后对队列进行遍历,分别计算源点的上下左右位置是否为-1,如果是则将该位置的值置为源加1,然后将这个点放入到队列中,相当与源。当队列为空时,跳出循环,就可到得到结果。
func updateMatrix(mat [][]int) [][]int {
if len(mat)<=0{
return nil
}
// 使用多源广度优先算法进行遍历:队列
queue := make([][]int,0)
// 先获取所有零的位置,每个零都是一个源,来进行广度遍历,使用-1表示没有被访问过的值
for i:=0;i<len(mat);i++{
for j:=0;j<len(mat[i]);j++{
if mat[i][j] == 0{
tmp := []int{i,j}
queue = append(queue,tmp)
}else if mat[i][j] == 1{
mat[i][j] = -1
}
}
}
row := len(mat)
col := len(mat[0])
// 每个点的上下左右位置的表示
direction := [][]int{{0,-1},{0,1},{-1,0},{1,0}}
for len(queue)!=0{
tmp := queue[0]
queue = queue[1:] // 表示从队列中获取元素
// 表示这个点的上下左右的位置
for i:=0;i<len(direction);i++{
// 这里就是表示的是上下左右的位置
x := tmp[0] + direction[i][0]
y := tmp[1] + direction[i][1]
if x>=0&&x<row&&y>=0&&y<col&&mat[x][y]==-1{
mat[x][y] = mat[tmp[0]][tmp[1]] + 1
queue = append(queue,[]int{x,y})
}
}
}
//for i:=0;i<len(mat);i++{
// log.Println(mat[i])
//}
return mat
}
原文:https://www.cnblogs.com/MyUniverse/p/14840967.html