假设我们当前遇到了这样的一个问题:有一个文本串 \(S\) 和一个模式串 \(P\) ,现在要查找 \(P\) 在 \(S\) 中的位置,该如何实现?
如果用暴力匹配的思路,假设现在 \(S\) 匹配到 \(i\) 位置, \(P\) 匹配到 \(j\) 位置,则有:
理清楚了暴力匹配算法的流程以及其内在的逻辑,我们就可以写出暴力匹配的代码,如下:
int match(char* s, char* p)
{
int slen = strlen(s), plen = strlen(p);
int i = 0, j = 0;
while(i < slen && j < plen)
{
if(s[i] == p[j]) i++, j++;
// 如果当前字符匹配成功,则i++, j++.
else i = i - j + 1, j = 0;
// 如果失配,令i = i - (j-1), j = 0.
}
if(j == plen) return i-j;
else return -1;
// 匹配成功返回P在S中的位置(即i-j),否则返回-1.
}
从中我们不难发现,此暴力匹配算法的时间复杂度是非常高的且并没有有效地利用到之前已匹配完的结果,那么有没有一种算法能让 \(i\) 不回溯,只需要移动 \(j\) 呢?
答案是肯定的. 这个算法就是本文主旨—— KMP 算法.
Knuth-Morris-Pratt 字符串查找算法,简称为“KMP算法”,由 \(Donald ~ Knuth\) 、\(Vaughan ~ Pratt\)、和 \(James ~ H. ~ Morris\) 三人于 \(1997\) 年联合发表,常用于在一个文本串 \(S\) 内查找一个模式串 \(P\) 的出现位置.
下面先直接给出 KMP 算法的具体流程:
其中,\(nxt[i]\) 表示 \(i\) 之前 的字符串中最长的相同的 真前缀 和 真后缀 的长度,称为 前缀函数.
例如:\(nxt[j] = k\) 就代表着在 \(j\) 之前的字符串中有最大长度为 \(k\) 的相同的真前缀和真后缀.
对于字符串ABCDABD,它的前缀函数如下:
| 模式串 | A | B | C | D | A | B | D |
|---|---|---|---|---|---|---|---|
| 前缀函数值 | \(-1\) | \(0\) | \(0\) | \(0\) | \(0\) | \(1\) | \(2\) |
根据上表,可以得出结论——失配时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的前缀函数值.
此也意味着在某个字符失配时,该字符对应的 \(nxt\) 值会告诉你在下一步的匹配中,模式串 \(P\) 应该跳到哪一个位置(也即 \(nxt[j]\) 的位置). 如果 \(nxt[j] = 0\) 或 \(nxt[j] = -1\),则跳到 \(P\) 的开头字符,而若 \(nxt = k~(k>0)\),则代表下次跳到 \(j\) 之前的某一个字符,而不是跳到开头,并且具体跳过了 \(k\) 个字符.
转换成代码表示,即为:
int kmp(char* s, char* p)
{
int i = 0, j = 0, slen = strlen(s), plen = strlen(p);
while(i < slen && j < plen)
{
if(j == -1 || s[i] == p[j]) i++, j++; //如果j = -1,或者当前字符匹配成功(也即S[i] == P[j]),令i++,j++.
else j = nxt[j] //如果j != -1,且当前字符匹配失败(也即S[i] != P[j]),则令 i 不变,j = nxt[j].
}
if(j == plen) return i-j;
else return -1;
}
基于之前的理解,我们不难知道:可以采用 递推 的方法来计算前缀函数.
举个例子,如下图,根据模式串ABCDABD的 \(nxt\) 数组可知失配位置的字符D对应的 \(nxt\) 值为2,代表字符D前有长度为 \(2\) 的相同真前缀和真后缀(即AB),失配后,模式串需要向右移动 \(j - next [j] = 6 - 2 =4\) 位.
向右移动 \(4\) 位后,模式串 \(P\) 中的字符 \(C\) 继续跟文本串匹配.
对于模式串 \(P\) 的前 \(j+1\) 个序列字符:
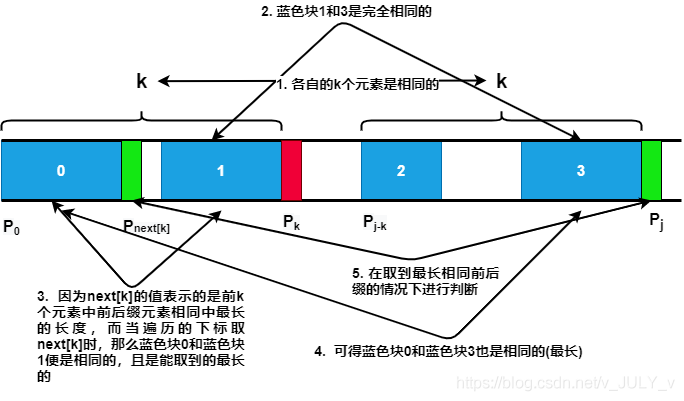
综上,可以通过递推求得前缀函数,代码如下所示:
void getnxt(char* p, int nxt[])
{
int plen = strlen(p);
nxt[0] = -1;
int k = -1, j = 0;
while(j < plen-1)
{
if(k == -1 || p[j] = p[k])
{
j++, k++;
nxt[j] = k;
}
else k = nxt[k];
}
}
至此,前缀函数的求解算是有了办法,但是这其中还是有一点小问题—— \(nxt\) 数组还可优化.
当 \(P[j] \ne S[i]\) 时,下次匹配必然是 \(P[nxt[j]]\) 去和 \(S[i]\) 匹配,若 \(P[j] = P[nxt[j]]\),则必然导致后一步的匹配失败,所以不能允许 \(P[j] = P[nxt[j]]\).
那么如果出现了 \(P[j] = P[nxt[j]]\) 怎么办呢?我们需要再次递归,令 \(nxt[j] = nxt[nxt[j]]\).
所以,我们得修改下求 \(nxt\) 数组的代码:
void getnxt(char* p, int nxt[])
{
int plen = strlen(p);
nxt[0] = -1;
int k = -1, j = 0;
while(j < plen-1)
{
if(k == -1 || p[j] = p[k])
{
j++, k++;
if(p[j] != p[k]) nxt[j] = k;
else nxt[j] = nxt[k];
}
else k = nxt[k];
}
}
优化后的 \(nxt\) 数组在前缀函数的基础上,更加适应 KMP 算法.
通过 KMP 的算法流程以及 \(nxt\) 数组的求解,我们可以知道:
设文本串的长度为 \(n\),模式串的长度为 \(m\),那么匹配的时间复杂度为 \(O(n)\),加上计算 \(nxt\) 数组的 \(O(m)\),总的时间复杂度为 \(O(n+m)\).
原文:https://www.cnblogs.com/chy12321/p/14840940.html