数据挖掘实践（54）：xgboost 推导与实例

来源：https://blog.csdn.net/weixin_41580067/article/details/86220782

一 XGBoost实例演练

上面的算法流程有些抽象，所以我们还是以实例来一步一步的实现XGBoost,数据集如下表：

1、生成第一颗树

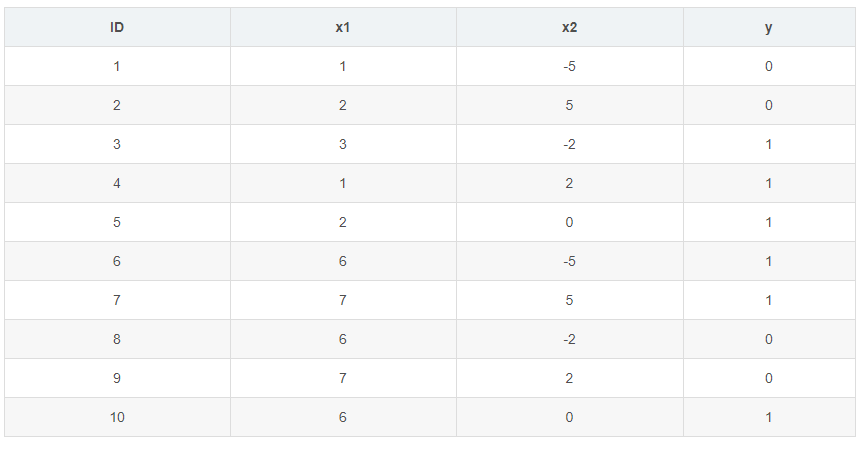
回顾我们上面的原理分析，对该结点是否划分的准则是计算增益：

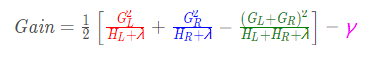
 对每一个样本求出其一阶、二阶导数的值：

 计算步骤如下：
对于ID=1的样本（其他样本计算类似）

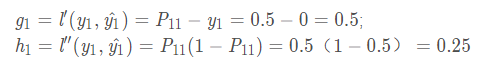
接下来我们需要在特征x1、x2中寻找最佳划分点.

以x1为例：我们需要将x1的特征值从小到大排列，一共有{ 1 , 2 , 3 , 6 , 7 } \left \{ 1,2,3,6,7\right \}{1,2,3,6,7} 5中取值。

当以特征值为1作为划分点时（x1<1）:

 最后计算增益：

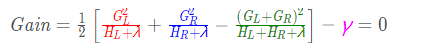
 这是显然的，因为左子树是空集，相当于没有对数据集进行划分

当以特征值为2作为划分点时（x1<2）:

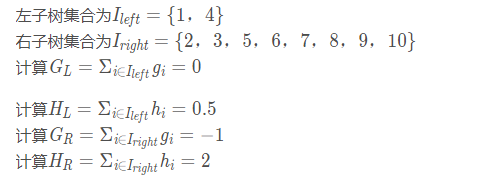
 最后计算增益：

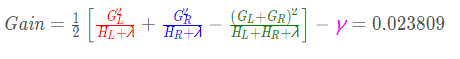
 依次算出x1的各个特征值的参数，如下表：

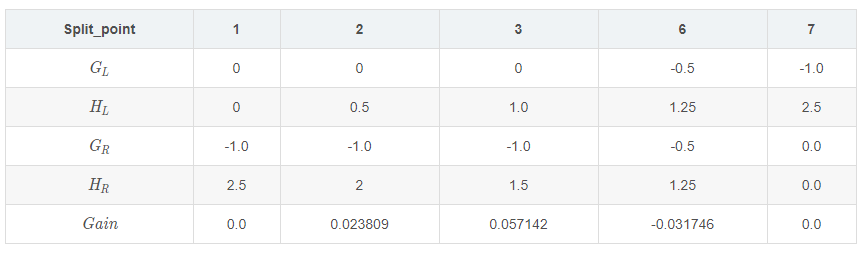
 因此x1的特征下的最佳划分点为x1<3，此时得到的增益最大。

若以x2为例：x2的可能取值排序为{ ? 5 ， ? 2 ， 0 ， 2 ， 5 } \left \{ -5，-2，0，2，5\right \}{?5，?2，0，2，5}

当以特征值为-5作为划分点时（x2<-5):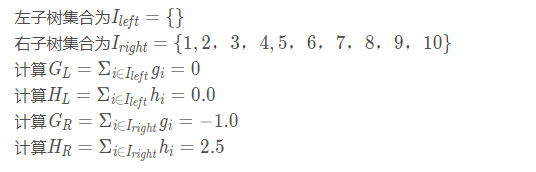

 最后计算增益：

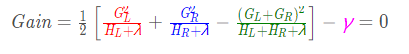
 当以特征值为-2作为划分点时（x2<-2):

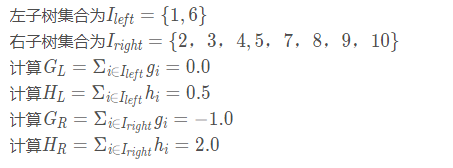
 最后计算增益：

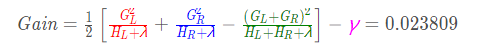
 然后也是依次计算出特征x2的各个划分点的参数与增益值，列表如下：

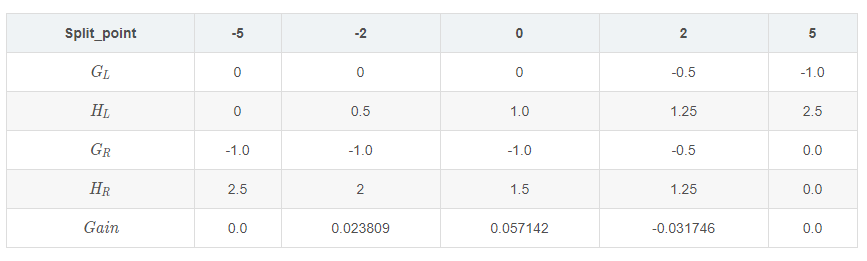
 因此对特征x2而言，最佳划分点位x2<0

因为x1与x2的最佳划分点的增益值相同，所以我们选取x1<3作为最佳划分点即可。

2、生成第二棵树

 由加法模型知：

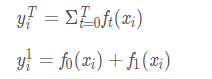
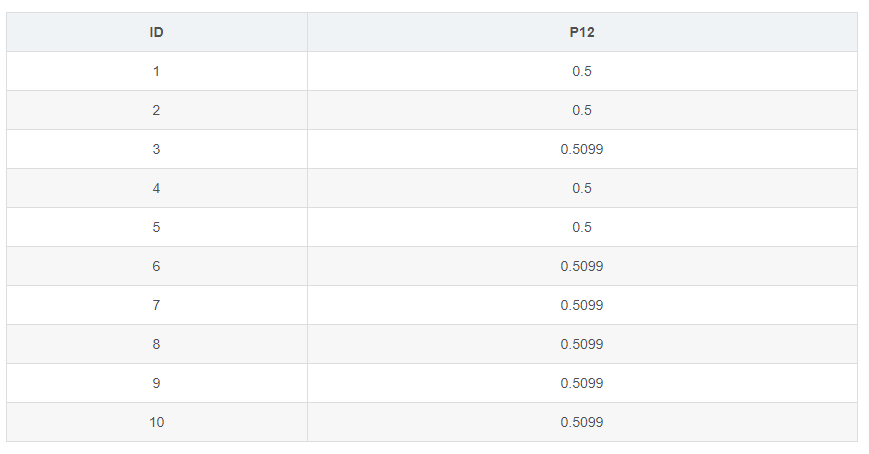
 后面的树的生成与第一颗树一模一样，记得最后需要对预测值做映射。

数据挖掘实践（54）：xgboost 推导与实例

原文：https://www.cnblogs.com/qiu-hua/p/14847710.html