归并排序

全文引用：图解排序算法之归并排序
归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

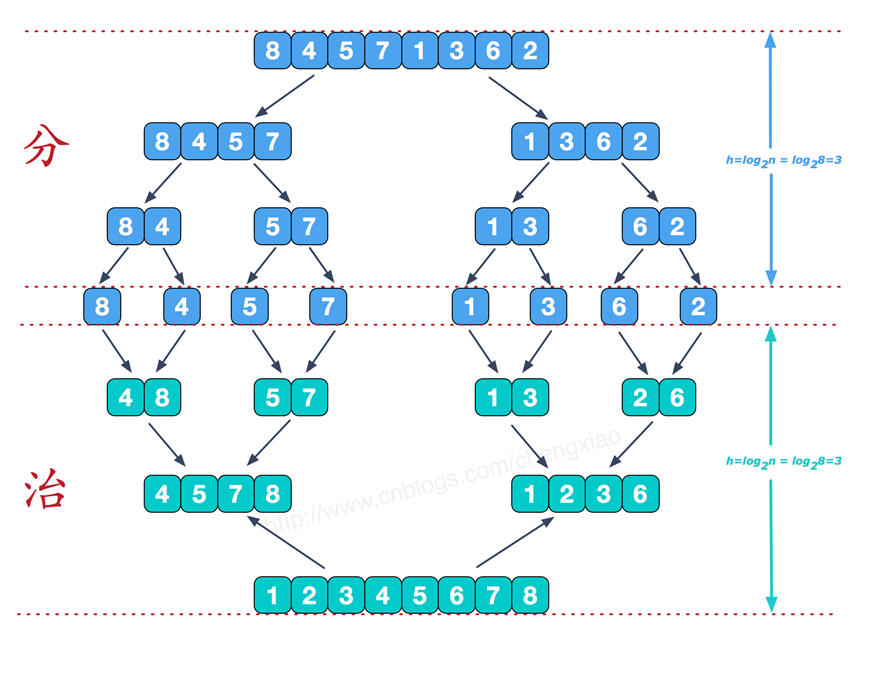
合并两个有序序列
我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

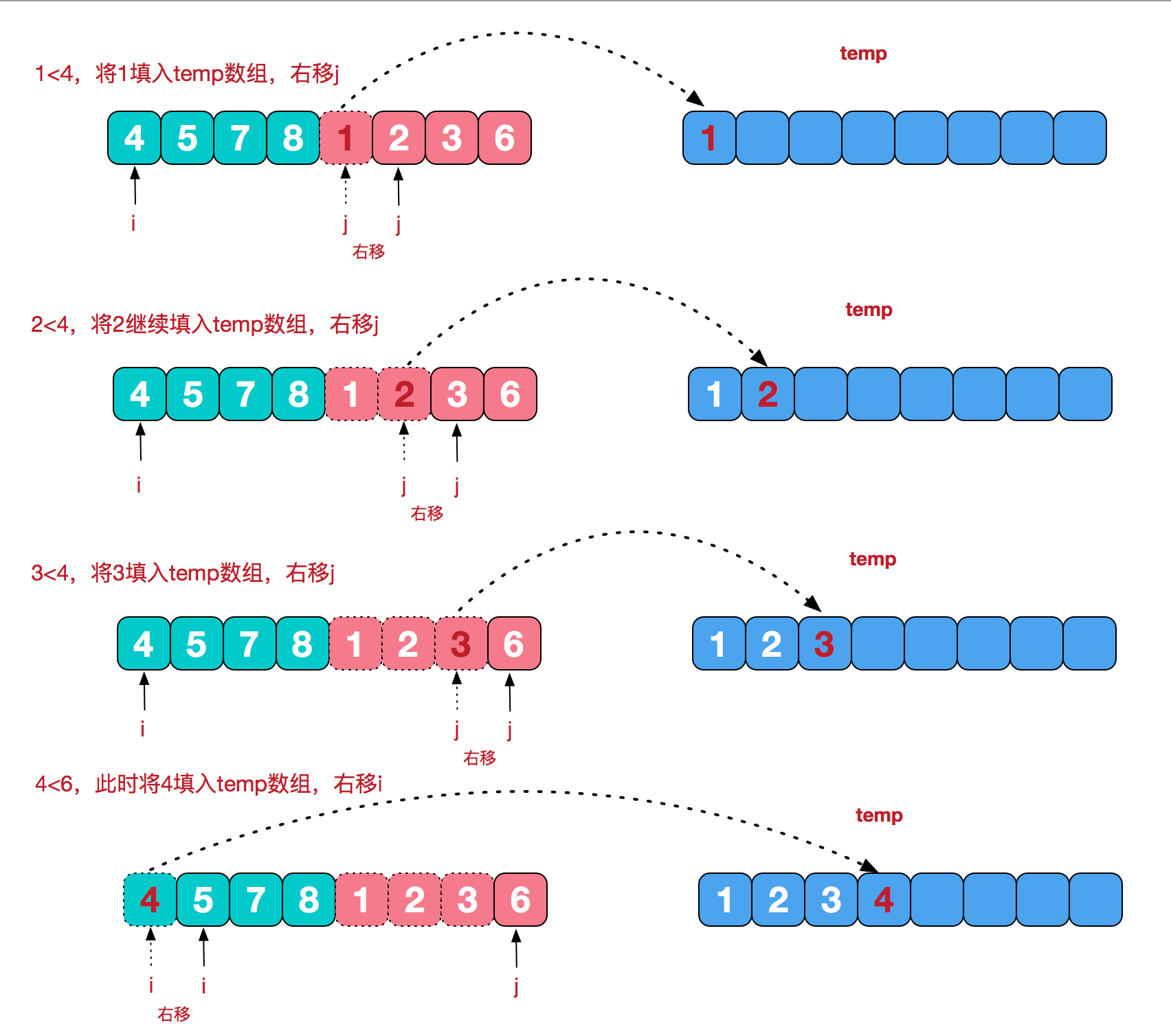
归并排序实现：
时间复杂度：n个数据大致会分割logN层，每层merge总复杂度O(n),时间复杂度O(nlogn)。
空间复杂度：O(n）

class Solution {
public:

    void merger(vector<int>& nums, int left, int mid, int right)
    {
        vector<int> temp(right - left + 1);
       int l = left;//左序列指针
       int r = mid + 1; //右序列指针
       int t = 0;//临时数组指针
       while(l <= mid && r <= right)
       {
           if(nums[l] <= nums[r])
           {
               temp[t++] = nums[l++];
           }else{
               temp[t++] = nums[r++];
           }
       }
       while(l <= mid) //将左边剩余元素填入temp中
       {
           temp[t++] = nums[l++];
       }
       while(r <= right) //将右边剩余元素填入temp中
       {
           temp[t++] = nums[r++];
       }

       //将temp中的元素拷贝到原数组中
       for(int i = 0; i < t; i++)
       {
           nums[left++] = temp[i];
       }



    }
    void mergerSort(vector<int>& nums, int left, int right)
    {
        if(left < right)
        {
            int mid = left + (right - left) / 2;
            mergerSort(nums, left, mid); //归并左边的序列，使左边有序
            mergerSort(nums, mid + 1, right); //归并右边的序列，使右边有序
            merger(nums, left, mid, right); //合并两个有序序列
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        vector<int> temp(nums.size());
        mergerSort(nums, 0, nums.size() - 1);
        return nums;
    }
};

归并排序

原文：https://www.cnblogs.com/ZigHello/p/14852603.html