1. 问题

给定字符集C={x1,x2,…,xn}和每个字符的频率f(xi)，求关于C的一个最优前缀码。

2. 解析

Note:每次构造二叉树时已按字母频率递增顺序排好序

步骤：每次构造二叉树将频率低的两棵树进行合并

1.我们借用上面的例子得到初始字母叶节点：

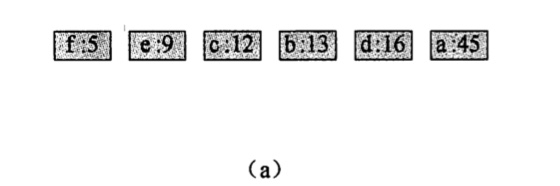
2.f 和 e 合并：

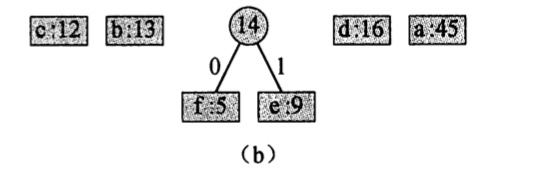
3.c 和 b 合并：

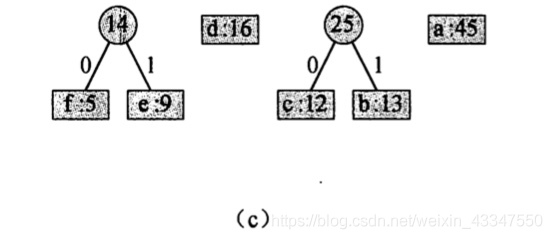
4. 14 和 d 合并：

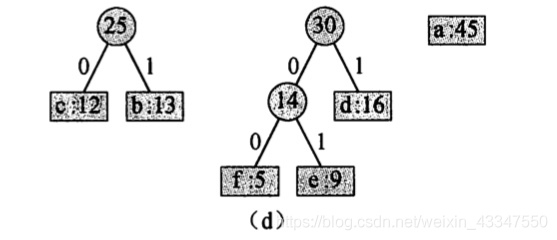
5. 25 和 30 合并：

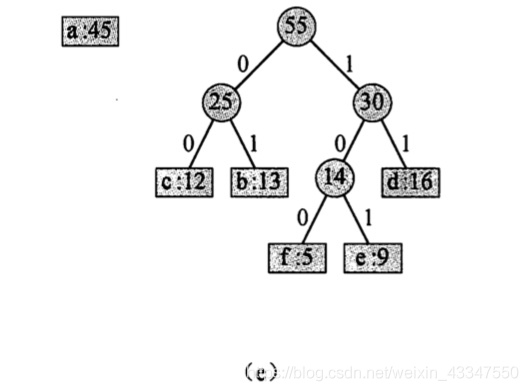
6. 45 和 55 合并，最终得到完整的赫夫曼树：

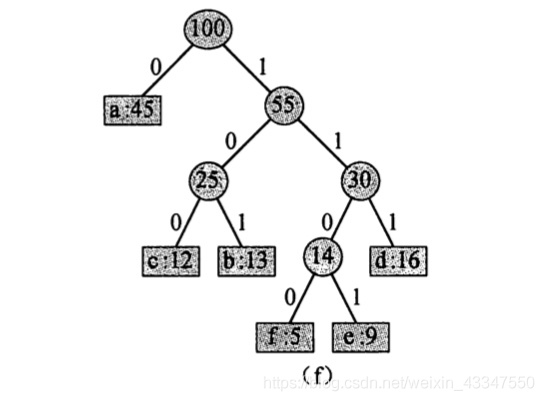
因此得到哈夫曼编码为：

a 的编码为： 0

b 的编码为： 101

c 的编码为： 100

d 的编码为： 111

e 的编码为： 1101

f 的编码为： 1100

3. 设计

算法 L o a d i n g ( W , c 1 ) ；?

   S o r t ( W )；

        B ← c 1 ; b e s t ← c 1 ; i ← 1 ;

4      while?i ≤ n do

??       if 装入i ii后重量不超过c 1

?         ? then B ← B ? w i ; x [ i ] ← 1 ; i ← i + 1 ;

?         else x [ i ] ← 0 ; i ← i + 1 ;

        if B <best  

            then记录解; b e s t ← B ;

        B a c k t r a c k ( i ) ;

       if i = 1

            then return 最优解

      else goto 4.

4. 分析

首先按照物品体积进行排序，调用sort() 函数，其最优时间复杂度为O(n),最差时间复杂度为 O(n logn),平均时间复杂度为O(n logn), 其中按照 贪心策略寻找最优解的 for 语句的时间复杂度为均为 O(n),因此时间复杂度为 O(n+nlogn)。

5. 源码

[github源码地址]

最优前缀码

原文：https://www.cnblogs.com/zs0618/p/14856414.html