布隆过滤器

布隆过滤器

　　布隆过滤器主要用于判断一个元素是否在一个集合中，它可以使用一个位数组简洁的表示一个数组。它的空间效率和查询时间远远超过一般的算法，但是它存在一定的误判的概率，适用于容忍误判的场景。如果布隆过滤器判断元素存在于一个集合中，那么大概率是存在在集合中，如果它判断元素不存在一个集合中，那么一定不存在于集合中。常常被用于大数据去重。

算法思想

　　布隆过滤器算法主要思想就是利用k个哈希函数计算得到不同的哈希值，然后映射到相应的位数组的索引上，将相应的索引位上的值设置为1。判断该元素是否出现在集合中，就是利用k个不同的哈希函数计算哈希值，看哈希值对应相应索引位置上面的值是否是1，如果有1个不是1，说明该元素不存在在集合中。但是也有可能判断元素在集合中，但是元素不在，这个元素所有索引位置上面的1都是别的元素设置的，这就导致一定的误判几率。布隆过滤的思想如下图所示：

背景介绍

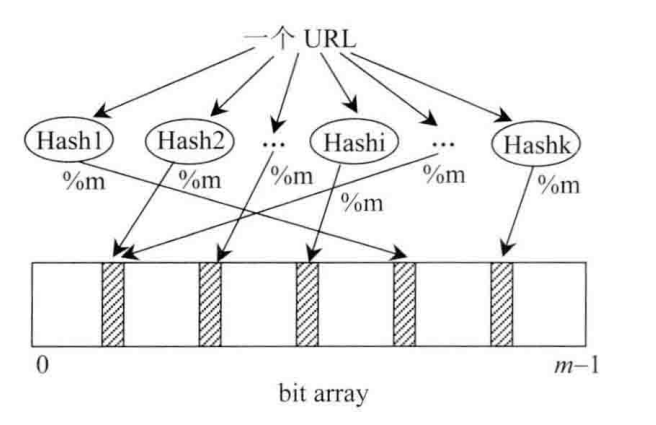
Bloom filter(后面简称BF)是Bloom在1970年提出的二进制向量数据结构。通俗来说就是在大数据集合下高效判断某个成员是否属于这个集合。BF其优点在于：

• 插入和查询复杂度都是O(n)
• 空间利用率极高。

例子1：

像Yahoo这类的公共邮件服务提供商，总是需要过滤垃圾邮件。 假设有50亿个邮件地址，需要存储过滤的方法有：

1. 所有邮件地址都存储到数据库。
   缺点：每次都需要查询数据库，效率低。
2. 使用Hashtable保存到内存里，接近O(1)的查询效率。
   缺点：太占内存，假定每个地址需要十六个字符，50亿个需要180G内存。
3. 创建位数组，将每个邮件地址用Hash函数映射到位数组中的某一位。
   缺点： 单个Hash函数冲突太高，会发生多个邮件会映射到同一位上。

而使用BF可以最大限度避免上述缺点，使其可以在更小空间上，进行高效插入和查询。

例子2：

经常使用缓存的肯定知道，命中率是个永远的话题。 特别是在分布式缓存中，每次不命中就意味着一次跨网络通信的浪费，无故增加缓存服务器压力。使用BF可以在很大程度上提高缓存命中率。

算法原理

BF很合适解决类似上面的问题。 BF和例子1中的第三种方法非常类似了。不同的是，BF对同一个邮件地址使用多个不同的Hash函数，再去映射位数组的中对应位置。

算法步骤：

1. 创建长度为m的位数组，全部置为0。
2. 取出邮件地址集合(m)中的某一个地址(a), 分别使用k个hash函数对a计算。
3. 将结果分别映射到位数组中，并设置为1。
4. 其他成员依次处理。

以函数个数k=8来算，50亿个邮件地址只需要5G内存足够了，比例子1中方法2节省32倍空间。

当查询成员a时是否在垃圾邮件集合m中时，使用同样k个hash函数进行计算，如果k个结果在位数组中的位值都是1，则判断a属于m集合中，即a邮件地址属于垃圾邮件地址集合m(a∈m)。

关于例子2，可以将所有key存储到本地内存中，每次远程获取缓存时，优先在内存集合中判断是否存在。

1. 存在？去远程获取实际缓存内容。
2. 不存在？直接返回，无需再去远程缓存服务器判断。

这样能极大提高缓存命中率，因为BF存在误判率，所有并不能达到100%(在key的数量级不高时，用其他方法全存下来也可以)。

误判率

因为BF使用Hash函数来取得成员的特征(可理解为成员的指纹信息)，并没有在位数组中存储集合内的实际数据内容，所以空间利用率极高，但存在个潜在问题，就是查询某个成员是否属于集合时，会发生误判(False positive)。 也就是说，某个成员实际不在集合中，但BF会得出在集中的结论。 所以BF适用于允许发生一定误判的场景，如例子1、2中少量过滤失败或去服务器拿都是可以接受的。

为什么会有误判?

假定有一个长度12的位数组，使用3个hash函数，根据算法计算成员a得出3、7、11位置，并在位数组中设置为1。 另外个成员b根据算法也计算得出3、7、11，去位数组检查其位值时，就发现3、7、11都为1是存在的，而实际不存在(1是成员a设置的)，此时就发生了误判现象。

BF会发生误判，但不会发生漏判(False Negative)，即成员实际在集合中，那么BF一定能判断出在集合中，因为成员对应的位置都设置为1了。

可控制性

根据其数组长度m、集合大小n、hash函数个数k、误判率p，简单得出下：

1. 其他不变，集合大小n越大，越多位被设置1，误判率p越大。
2. 其他不变，数组涨肚m越大，剩余为0的位越多，误判率p越小
3. 其他不变，添加时k越多，位数组越多被设置为1，即会增大误判率。查询时k越多，明显误判率可能就会越小。

hash函数个数取值公式 k = ln 2 * m/n 。

其他它关系公式见wiki。

BF改进 

基本的BF在使用时有个缺点：无法删除集合成员a，只能增加其成员并对其查询。 有一个很容易想到但错误的方法是：如果要删除成员a，那么先用k个hash函数对其计算，因为a已经是集合成员，那么其对应的位数组的位置一定被设置为1，所以只要将对应位置重新设置为0即可。   原因就是位数组的位置不但只提供给a使用，也给其他成员使用，一旦设置为0就会影响其他成员的使用。

比如上面中提高缓存命中率的例子，不能删除成员意味着实际缓存也不能删除。如果实际缓存删除了，而在集合中的数据无法删除，就会发生漏判现象。 这样的话就会大大限制BF的使用场景。

计数BF(count bloom filter)

计数BF是对基本BF的改进，使BF可以支持删除成员。  因为BF的基本单位是1个bit，只能表达2种状态，即存在、不存在。 如果把基本单位1bit拓展成多个bit，这样就能增加更多信息，表达出多种状态。

计数BF的基本单元由多个bit表示，一般情况为3、4个bit。  这样在添加时，在数组位置上的数值上加1即可，删除成员时-1即可。 查询集合成员时保持不变，只要数值不为0即认为成员是存在的。

计数BF使基本BF有了更多应用场景。 同样由于用了多个bit来表示，对应数组大小也相应增加，如果用3bit作为基本单位，那么数组大小对应增加了3倍。

BF是大数据处理的利器，其使用场景非常多：

• Google的爬虫重复URL检测。
• 黑名单验证。
• 例子中的缓存命中率，垃圾邮件过滤。
• 内存挡一层，减轻db空查压力。
• hbase、LevelDB内部使用。

C#实现布隆过滤器

public class BloomFilter
    {
        public BitArray _BloomArray;
        public Int64 BloomArryLength { get; }
        public Int64 BitIndexCount { get; }

        /// <summary>
        /// 初始化
        /// </summary>
        /// <param name="BloomArryLength">布隆数组的大小</param>
        /// <param name="bitIndexCount">hash次数</param>
        public BloomFilter(int BloomArryLength,  int bitIndexCount)
        {
            _BloomArray = new BitArray(BloomArryLength);
            this.BloomArryLength = BloomArryLength;
            this.BitIndexCount = bitIndexCount;
        }


        public void Add(string str)
        {
            var hashCode = GetHashCode(str);
            Random random = new Random(hashCode);
            for (int i = 0; i < BitIndexCount; i++)
            {
                var c = random.Next((int)(this.BloomArryLength - 1));
                _BloomArray[c] = true;
            }
        }

        public bool isExist(string str)
        {
            var hashCode = GetHashCode(str);
            Random random = new Random(hashCode);
            for (int i = 0; i < BitIndexCount; i++)
            {
                if (!_BloomArray[random.Next((int)(this.BloomArryLength - 1))])
                {
                    return false;
                }
            }
            return true;
        }

        public int GetHashCode(object value)
        {
            return value.GetHashCode();
        }
    }

客户端

BloomFilter bf = new BloomFilter(1000000, 3);
            for (int i = 0; i < 100000; i++)
            {
                bf.Add(i.ToString());
            }
            int errorCount = 0;
            for (int i = 100000; i < 110000; i++)
            {

                if (bf.isExist(i.ToString()))
                {
                    errorCount++;
                }
            }

布隆过滤器

原文：https://www.cnblogs.com/tuyile006/p/14862025.html