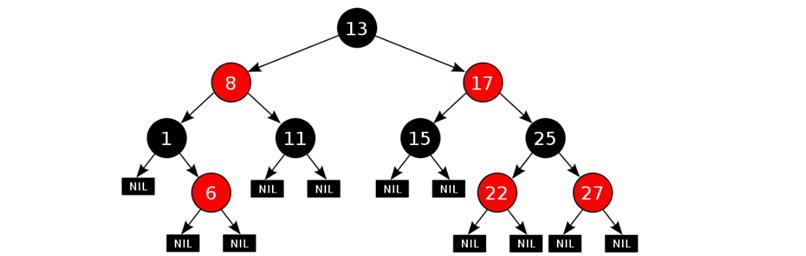
1. 每一个节点或是红色的,或者是黑色的
2. 根节点必须是黑色
3. 如果一个节点没有子节点或者父节点,则该节点相应的指针属性值为Nil,这些Nil视为叶节点,每个叶节点(Nil)是黑色的
4. 如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连 的情况)
5. 对每一个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点
红黑树添加节点的颜色默认为红色(默认红色效率高)
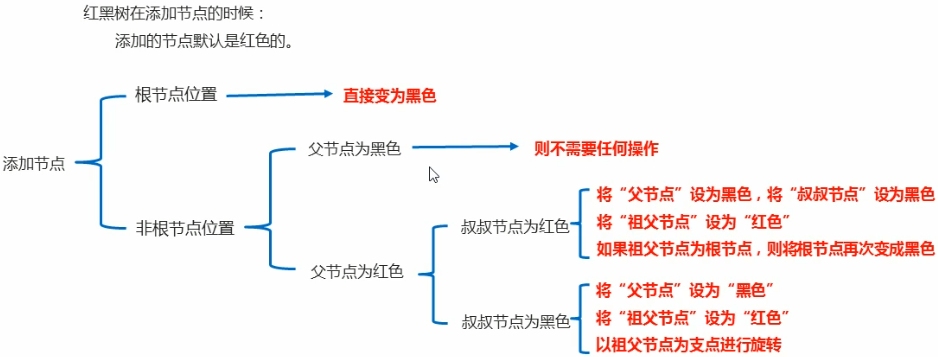
红黑规则图中名词说明:
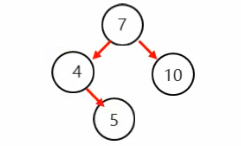
对于5节点来说(如上图),4节点是5节点的父节点,10节点是5节点的叔叔节点,7节点是5节点的祖父节点(这里暂时这么定义)
将下面数据按照红黑树规则依次添加到树中(默认为红色)

则添加流程为:
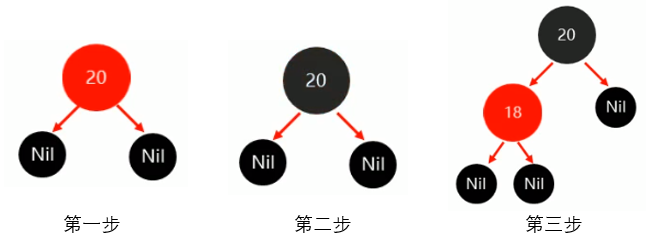
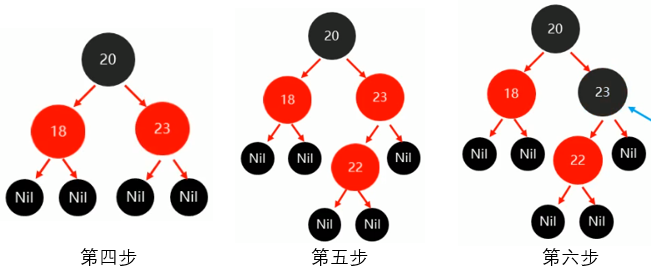
第一步:添加20为根节点
第二步:根节点必须为黑色,红色改为黑色
第三步:添加18比20小,作为20的左子节点,该数(18)父节点(20)为黑色,不用做任何操作
第四步:23比20大,作为20的右子节点,该数(23)父节点(20)为黑色,不用做任何操作
第五步:添加22,22比20大,作为20的右节点,由于右结点有数据,再和20右结点数据23相比较,22比23小,则作为23的左子节点(此为二叉查找树添加数据规则,我前篇有介绍,后面不再讲述)
第六步:由于23和22都是红色,由于不能出现两个红色节点相连的情况。此时符合父节点为红色,叔叔节点为红色情况,按照(规则-)将“父节点23”设为黑色
第七步:(规则-)将22的叔叔节点18变为黑色
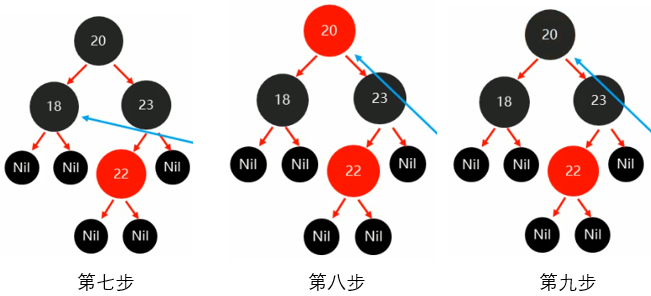
第八步:(规则-)将22的祖父节点20变为红色
第九步:(规则-)如果22的祖父节点20为根节点,则将根节点再次变为黑色
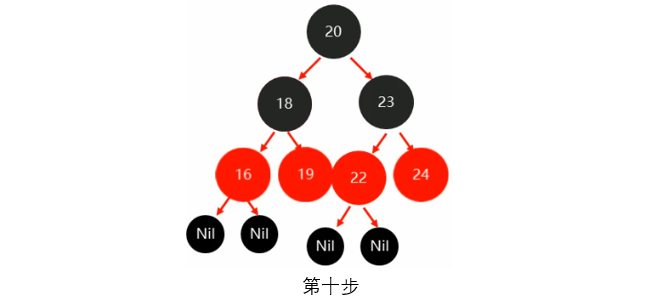
第十步:将最后的16、24和19依次添加到树中,由于不违反红黑树规则,则不做任何操作
现在已经是一个完整的红黑树了,不过还有更加复杂的情况出现。继续添加数据15和14在此树中,看结果会是什么样子

将数据15和14按照顺序添加进树中
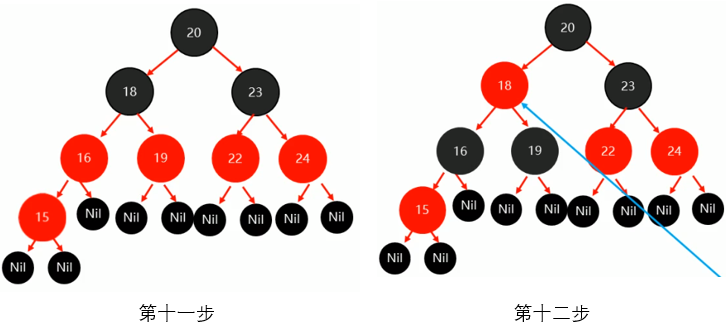
第十一步:将15添加到树中相应位置
第十二步:15的父节点16为红色,15的叔叔节点19也为红色,所以符合父节点为红色,叔叔节点也为红色情况,按照规则,将父节点16改为黑色,将叔叔节点19改为黑色
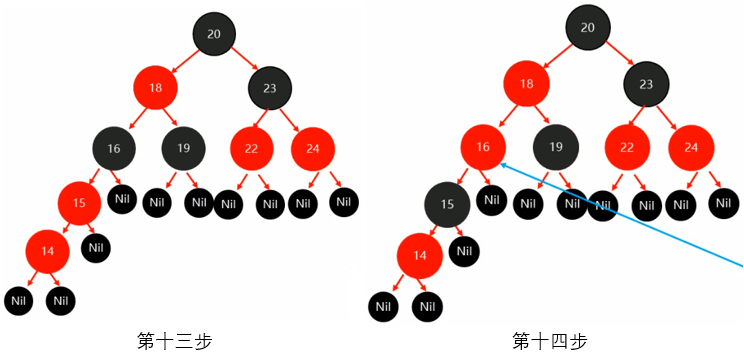
第十三步:继续添加14节点到相应位置
第十四步:由于14的父节点15为红色,叔叔节点Nil为黑色,符合父节点为红色,叔叔节点为黑色情况,所以按照规则将父节点15改为黑色,将祖父节点16改为红色
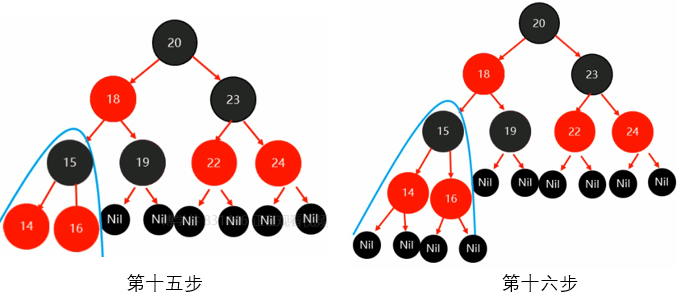
第十五步:以祖父节点16为支点进行旋转(此时就把16作为根节点,除了16的子孙节点外都不看,如果进行旋转,可看出为右旋,上一篇有讲述),旋转时Nil先忽略,旋转后再补齐
第十六步:此时已经是一个完整的红黑树
原文:https://www.cnblogs.com/bluecore/p/14862201.html