程序来自Program Creek
前
Preorder binary tree traversal is a classic interview problem about trees. The key to solve this problem is to understand the following:
It is not obvious what preorder for some strange cases. However, if you draw a stack and manually execute the program, how each element is pushed and popped is obvious.
The key to solve this problem is using a stack to store left and right children, and push right child first so that it is processed after the left child.
1 public class TreeNode { 2 int val; 3 TreeNode left; 4 TreeNode right; 5 TreeNode(int x) { val = x; } 6 } 7 8 public class Solution { 9 public ArrayList<Integer> preorderTraversal(TreeNode root) { 10 ArrayList<Integer> returnList = new ArrayList<Integer>(); 11 12 if(root == null) 13 return returnList; 14 15 Stack<TreeNode> stack = new Stack<TreeNode>(); 16 stack.push(root); 17 18 while(!stack.empty()){ 19 TreeNode n = stack.pop(); 20 returnList.add(n.val); 21 22 if(n.right != null){ 23 stack.push(n.right); 24 } 25 if(n.left != null){ 26 stack.push(n.left); 27 } 28 29 } 30 return returnList; 31 } 32 }
中
The key to solve inorder traversal of binary tree includes the following:
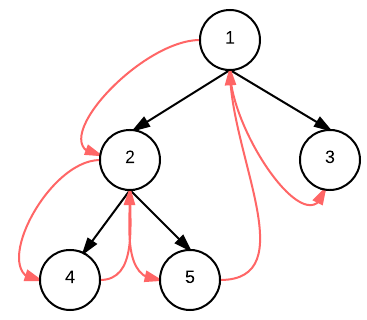
1 //Definition for binary tree 2 public class TreeNode { 3 int val; 4 TreeNode left; 5 TreeNode right; 6 TreeNode(int x) { val = x; } 7 } 8 9 public class Solution { 10 public ArrayList<Integer> inorderTraversal(TreeNode root) { 11 // IMPORTANT: Please reset any member data you declared, as 12 // the same Solution instance will be reused for each test case. 13 ArrayList<Integer> lst = new ArrayList<Integer>(); 14 15 if(root == null) 16 return lst; 17 18 Stack<TreeNode> stack = new Stack<TreeNode>(); 19 //define a pointer to track nodes 20 TreeNode p = root; 21 22 while(!stack.empty() || p != null){ 23 24 // if it is not null, push to stack 25 //and go down the tree to left 26 if(p != null){ 27 stack.push(p); 28 p = p.left; 29 30 // if no left child 31 // pop stack, process the node 32 // then let p point to the right 33 }else{ 34 TreeNode t = stack.pop(); 35 lst.add(t.val); 36 p = t.right; 37 } 38 } 39 40 return lst; 41 } 42 }
后
The key to to iterative postorder traversal is the following:
As we go down the tree, check the previously visited node. If it is the parent of the current node, we should add current node to stack. When there is no children for current node, pop it from stack. Then the previous node become to be under the current node for next loop.
1 //Definition for binary tree 2 public class TreeNode { 3 int val; 4 TreeNode left; 5 TreeNode right; 6 TreeNode(int x) { val = x; } 7 } 8 9 10 public class Solution { 11 public ArrayList<Integer> postorderTraversal(TreeNode root) { 12 13 ArrayList<Integer> lst = new ArrayList<Integer>(); 14 15 if(root == null) 16 return lst; 17 18 Stack<TreeNode> stack = new Stack<TreeNode>(); 19 stack.push(root); 20 21 TreeNode prev = null; 22 while(!stack.empty()){ 23 TreeNode curr = stack.peek(); 24 25 // go down the tree. 26 //check if current node is leaf, if so, process it and pop stack, 27 //otherwise, keep going down 28 if(prev == null || prev.left == curr || prev.right == curr){ 29 //prev == null is the situation for the root node 30 if(curr.left != null){ 31 stack.push(curr.left); 32 }else if(curr.right != null){ 33 stack.push(curr.right); 34 }else{ 35 stack.pop(); 36 lst.add(curr.val); 37 } 38 39 //go up the tree from left node 40 //need to check if there is a right child 41 //if yes, push it to stack 42 //otherwise, process parent and pop stack 43 }else if(curr.left == prev){ 44 if(curr.right != null){ 45 stack.push(curr.right); 46 }else{ 47 stack.pop(); 48 lst.add(curr.val); 49 } 50 51 //go up the tree from right node 52 //after coming back from right node, process parent node and pop stack. 53 }else if(curr.right == prev){ 54 stack.pop(); 55 lst.add(curr.val); 56 } 57 58 prev = curr; 59 } 60 61 return lst; 62 } 63 }
尚待实践和整理
原文:http://www.cnblogs.com/LolaLiu/p/3989251.html