设A1,A2,A3.......An为n个矩阵的序列,其中Ai为pi-1*pi阶矩阵,这个矩阵链的输入用向量p=<p0,p1,p2,....pn>给出。
给董向量p,确定一种乘法的次序,使得基本运算的总次数达到最小。
假设给定序列p=<100,10,20,5,100>
则A1=100*10,A2=10*20,A3=20*5,A4=5*100;
假设(((A1*A2)*A3)*A4)=100*10*20+100*20*5+100*5*100=8e4;
再比如A1*((A2*A3)*A4)=10*20*5+10*5*100+100*100*10=1e5+5e3;
再比如(A1*(A2*A3))*A4=10*20*5+100*10*5+100*5*100=5.6e4
可以很容易的观察出,如果排列的顺序是不同的那么所得到的答案相差会非常的大。
那么我们如何去求这个最优的答案,就可以用到动态规划。
我们可以先从小区间的最优解,再逐步扩大最终得到答案的最优解。
比如我设定相乘的长度为2时,那么我就可以用长度为1的两个最后解,再加上这次的最后解,得到答案的最优解。
比如我求a[l][r]=a[l][k]+a[k+1][l]+本次求解的最优解,我a[l][k]和a[k+1][l]都是在之前求过最优解,那么加上这次的最优解
显而易见就可以得到a[l][r]的最优解,本次最优解我只要去枚举哪一个矩阵生下来和他相乘就可以。
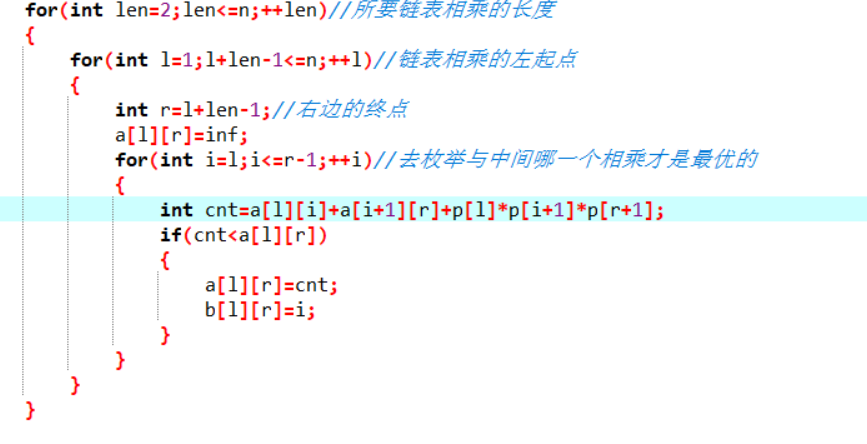
时间复杂度为O(n^3)
原文:https://www.cnblogs.com/passawayy/p/14879027.html