一、题目：

二、思路：

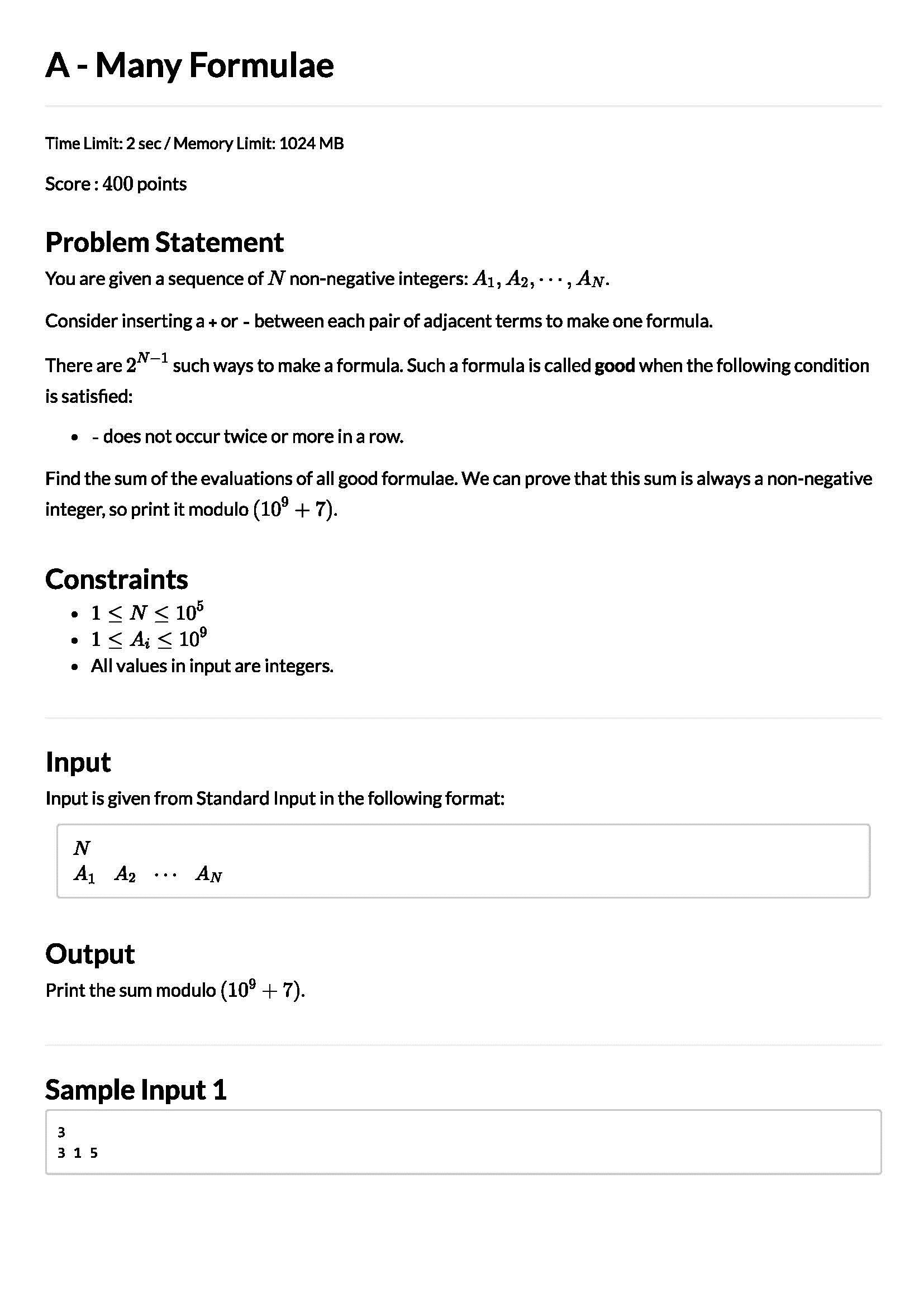
虽然这是一道A题，但是由于我太菜了?? ，居然没有想出来??。

现在来讲一下这题严谨的思路。

设 \(f[i,0/1]\) 表示当前填了 \(i\) 个符号，最后一个符号是 + 号还是 - 号的方案数。

我当时就只想到这里。

那么考虑最终第 \(i\) 个符号到底有几个 + 号和几个 - 号。

简单乘法原理。第一步，确定前 \(i\) 个符号的方案数；第二步，确定后 \(n - i - 1\) 个符号的方案数。

三、代码：

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;
#define FILEIN(s) freopen(s".in", "r", stdin);
#define FILEOUT(s) freopen(s".out", "w", stdout)
#define mem(s, v) memset(s, v, sizeof s)

inline int read(void) {
    int x = 0, f = 1; char ch = getchar();
    while (ch < ‘0‘ || ch > ‘9‘) { if (ch == ‘-‘) f = -1; ch = getchar(); }
    while (ch >= ‘0‘ && ch <= ‘9‘) { x = x * 10 + ch - ‘0‘; ch = getchar(); }
    return f * x;
}

const int mod = 1e9 + 7, maxn = 1e5 + 7;

int n;
long long dp[maxn][2], ans, a[maxn];

int main() {
    n = read();
    dp[0][1] = 1;
    for (int i = 1; i < n; ++ i) dp[i][0] = dp[i - 1][1], dp[i][1] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
    for (int i = 1; i <= n; ++ i) a[i] = read();
    (ans += (dp[n - 1][0] + dp[n - 1][1]) * a[1] % mod) %= mod;
    for (int i = 1; i < n; ++ i) {
        long long sum0 = dp[i][0] * dp[n - i - 1][1] % mod;
        long long sum1 = dp[i][1] * (dp[n - i - 1][0] + dp[n - i - 1][1]) % mod;
        (ans += (sum1 - sum0) * a[i + 1] % mod) %= mod;
    }
    if (ans < 0) ans += mod;
    printf("%lld\n", ans);
    return 0;
}

ARC122A Many Formulae 题解

原文：https://www.cnblogs.com/little-aztl/p/14879573.html