顺序(线性)查找
二分查找/折半查找
插值查找
斐波那契查找
1 public class SeqSearch { 2 3 public static void main(String[] args) { 4 int[] arr = { 1, 2, 3, 4, 5 };// 没有顺序的数组 5 int index = seqSearch(arr, -11); 6 if (index == -1) { 7 System.out.println("没有找到到"); 8 } else { 9 System.out.println("找到,下标为=" + index); 10 } 11 } 12 13 /** 14 * 这里我们实现的线性查找是找到一个满足条件的值,就返回 15 * 16 * @param arr 17 * @param value 18 * @return 19 */ 20 public static int seqSearch(int[] arr, int value) { 21 // 线性查找是逐一比对,发现有相同值,就返回下标 22 for (int i = 0; i < arr.length; i++) { 23 if (arr[i] == value) { 24 return i; 25 } 26 } 27 return -1; 28 } 29 30 }
二分查找算法的前提:数组必须是有序数组
二分查找算法思路分析(递归版):
定义两个辅助指针:left、right ,待查找的元素在 arr[left]~arr[right] 之间
left 初始值为 0 ,right 初始值为 arr.length - 1
将数组分成两半:int mid = (left + right) / 2; ,取数组中间值与目标值 findVal 比较
如果 mid > findVal ,说明待查找的值在数组左半部分
如果 mid < findVal ,说明待查找的值在数组右半部分
如果 mid == findVal ,查找到目标值,返回即可
何时终止递归?分为两种情况:
找到目标值,直接返回目标值 findVal ,结束递归即可
未找到目标值:left > right,这样想:如果递归至数组中只有一个数时(left == right),还没有找到目标值,继续执行下一次递归时, left 指针和 right 指针总有一个会再走一步,这时 left 和 right 便会错开,此时 left > right ,返回 -1 并结束递归表示没有找到目标值
1 //注意:使用二分查找的前提是 该数组是有序的. 2 public class BinarySearch { 3 4 public static void main(String[] args) { 5 6 int arr[] = { 1, 8, 10, 89, 1000, 1234 }; 7 int resIndex = binarySearch(arr, 0, arr.length - 1, 1000); 8 System.out.println("resIndex=" + resIndex); 9 10 } 11 12 // 二分查找算法 13 /** 14 * 15 * @param arr 数组 16 * @param left 左边的索引 17 * @param right 右边的索引 18 * @param findVal 要查找的值 19 * @return 如果找到就返回下标,如果没有找到,就返回 -1 20 */ 21 public static int binarySearch(int[] arr, int left, int right, int findVal) { 22 23 // 当 left > right 时,说明递归整个数组,但是没有找到 24 if (left > right) { 25 return -1; 26 } 27 int mid = (left + right) / 2; 28 int midVal = arr[mid]; 29 30 if (findVal > midVal) { // 向 右递归 31 return binarySearch(arr, mid + 1, right, findVal); 32 } else if (findVal < midVal) { // 向左递归 33 return binarySearch(arr, left, mid - 1, findVal); 34 } else { 35 36 return mid; 37 } 38 39 } 40 41 }
插值查找算法类似于二分查找, 不同的是插值查找每次从自适应 mid 处开始查找。
将折半查找中的求 mid 索引的公式 , low 表示左边索引 left ,high 表示右边索引 right ,key 就是前面我们讲的 findVal
图中公式:int mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low]) ;
对应前面的代码公式:
int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left])

1 public class InsertValueSearch { 2 3 public static void main(String[] args) { 4 5 int [] arr = new int[100]; 6 for(int i = 0; i < 100; i++) { 7 arr[i] = i + 1; 8 } 9 int index = insertValueSearch(arr, 0, arr.length - 1, 1); 10 System.out.println("index = " + index); 11 12 } 13 14 //编写插值查找算法 15 //说明:插值查找算法,也要求数组是有序的 16 /** 17 * 18 * @param arr 数组 19 * @param left 左边索引 20 * @param right 右边索引 21 * @param findVal 查找值 22 * @return 如果找到,就返回对应的下标,如果没有找到,返回-1 23 */ 24 public static int insertValueSearch(int[] arr, int left, int right, int findVal) { 25 26 System.out.println("插值查找次数~~"); 27 28 //注意:findVal < arr[left] 和 findVal > arr[right] 必须需要,否则我们得到的 mid 可能越界 29 // findVal < arr[left] :说明待查找的值比数组中最小的元素都小 30 // findVal > arr[right] :说明待查找的值比数组中最大的元素都大 31 if (left > right || findVal < arr[left] || findVal > arr[right]) { 32 return -1; 33 } 34 35 // 求出mid, 自适应,额,这不就是一次函数吗 36 // findVal = arr[left] 时,mid = left 37 // findVal = arr[right] 时,mid = right 38 int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]); 39 int midVal = arr[mid]; 40 if (findVal > midVal) { // 说明应该向右边递归 41 return insertValueSearch(arr, mid + 1, right, findVal); 42 } else if (findVal < midVal) { // 说明向左递归查找 43 return insertValueSearch(arr, left, mid - 1, findVal); 44 } else { 45 return mid; 46 } 47 48 } 49 }
黄金分割点是指把一条线段分割为两部分, 使其中一部分与全长之比等于另一部分与这部分之比。 取其前三位数字的近似值是 0.618。 由于按此比例设计的造型十分美丽, 因此称为黄金分割, 也称为中外比。 这是一个神奇的数字, 会带来意想不到的效果。
斐波那契数列 { 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 } 发现斐波那契数列的两个相邻数的比例, 无限接近 黄金分割值 0.618
那为什么一定要等分呐?能不能进行“黄金分割”?也就是 mid = left+0.618(right-left) ,当然mid 要取整数。如果这样查找,时间复杂性是多少?也许你还可以编程做个试验,比较一下二分法和“黄金分割”法的执行效率。
斐波那契查找算法又称为黄金分割法查找算法,斐波那契查找原理与前两种相似, 仅仅改变了中间结点(mid) 的位置,mid 不再是中间或由插值计算得到,而是位于黄金分割点附近, 即 mid = low + F(k-1) - 1
对 F(k)-1 的理解
由斐波那契数列 F[k]=F[k-1]+F[k-2] 的性质, 可以得到F[k]-1) =(F[k-1]-1) +(F[k-2]-1) + 1
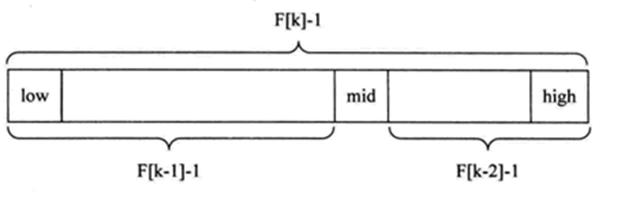
该式说明:只要顺序表的长度为 F[k]-1, 则可以将该表分成长度为 F[k-1]-1 和 F[k-2]-1 的两段 ,即如图所示。 从而中间位置为 mid=low+F(k-1)-1 ,类似的, 每一子段也可以用相同的方式分割
但顺序表长度 n 不一定刚好等于 F[k]-1, 所以需要将原来的顺序表长度 n 增加至 F[k]-1。 这里的 k 值只要能使得 F[k]-1 恰好大于或等于 n 即可
为什么数组总长度是 F(k) - 1 ,而不是 F(k) ?因为凑成 F(k-1) 才能找出中间值,如果数组长度为 F(k) ,而 F(k) = F(k-1) + F(k-2) ,咋个找中间值嘞?
为什么数组左边的长度是 F(k-1) - 1 ,数组右边的长度是 F(k-2) - 1 ?就拿个斐波那契数列来说:{ 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 } ,54 = 33 + 20 + 1 ,左边是不是 F(k-1) - 1 ,右边是不是 F(k-2) - 1 ,也恰好空出了一个中间值~~~
先根据原数组大小,计算斐波那契数列的得 k 值
数组扩容条件是:增大 k 值(索引从 0 开始),使得数组长度刚好大于或者等于斐波那契数列中的 F[k]-1 ,我们定义临时数组 temp ,temp 后面为 0 的元素都按照数组最大元素值填充
何时终止斐波那契查找?
找到目标值:直接返回目标值索引
没有找到目标值:low 指针和 high 指针相等或者擦肩而过,即 low >= high
low == high 时说明此时数组中只剩下一个元素(a[low] 或者 a[high])没有与目标值比较,并且此时 k 有可能等于 0 ,无法执行 mid = low + f[k - 1] - 1; 操作(k - 1 将导致数组越界)
解决办法:我们在程序的最后,将 a[low] 或者 a[high] 单独与目标值 value 进行比较即可,我是通过 Debug 解决数组越界异常的,我并没有想明白,但是不把 low == high 单独拎出来,就会抛异常,哎,烧脑壳~~~改天再想
mid 值怎么定?mid = low + f[k - 1] - 1 :用黄金分割点确定 mid 的值
左右两条路,你怎么选?
key < temp[mid] :目标值在黄金分割点的左边,看上面的图,应该是 k -= 1;
key > temp[mid] :目标值在黄金分割点的右边,看上面的图,应该是 k -= 2;
key = temp[mid] :找到目标值,因为数组经历过扩容,后面的值其实有些是多余的,mid 可能会越界(相对于原数组来说)
mid <= high :证明 mid 索引在原数组中,返回 mid
mid > high 时,证明 mid 索引已经越界(相对于原数组来说),返回 high
1 public class FibonacciSearch { 2 3 public static int maxSize = 20; 4 5 public static void main(String[] args) { 6 7 int[] arr = { 1, 2, 3, 4, 5 }; 8 System.out.println("index=" + fibSearch(arr, 5)); 9 10 } 11 12 // 因为后面我们mid=low+F(k-1)-1,需要使用到斐波那契数列,因此我们需要先获取到一个斐波那契数列 13 // 非递归方法得到一个斐波那契数列 14 public static int[] fib() { 15 int[] f = new int[maxSize]; 16 f[0] = 1; 17 f[1] = 1; 18 for (int i = 2; i < maxSize; i++) { 19 f[i] = f[i - 1] + f[i - 2]; 20 } 21 return f; 22 } 23 24 // 编写斐波那契查找算法 25 // 使用非递归的方式编写算法 26 /** 27 * 28 * @param a 数组 29 * @param key 我们需要查找的关键码(值) 30 * @return 返回对应的下标,如果没有-1 31 */ 32 public static int fibSearch(int[] a, int key) { 33 int low = 0; 34 int high = a.length - 1; 35 int k = 0; // 表示斐波那契分割数值的下标 36 int mid = 0; // 存放mid值 37 int f[] = fib(); // 获取到斐波那契数列 38 // 获取到斐波那契分割数值的下标 39 while (high > f[k] - 1) { 40 k++; 41 } 42 // 因为 f[k] 值 可能大于 a 的 长度,因此我们需要使用Arrays类,构造一个新的数组,并指向temp[] 43 // 不足的部分会使用0填充 44 int[] temp = Arrays.copyOf(a, f[k]); 45 // 实际上需求使用a数组最后的数填充 temp 46 // 举例: 47 // temp = {1,8, 10, 89, 1000, 1234, 0, 0} => {1,8, 10, 89, 1000, 1234, 1234, 48 // 1234,} 49 for (int i = high + 1; i < temp.length; i++) { 50 temp[i] = a[high]; 51 } 52 53 // 使用while来循环处理,找到我们的数 key 54 while (low < high) { // 只要这个条件满足,就可以找 55 mid = low + f[k - 1] - 1; 56 if (key < temp[mid]) { // 我们应该继续向数组的前面查找(左边) 57 high = mid - 1; 58 // 为甚是 k-- 59 // 说明 60 // 1. 全部元素 = 前面的元素 + 后边元素 61 // 2. f[k] = f[k-1] + f[k-2] 62 // 因为 前面有 f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3] 63 // 即 在 f[k-1] 的前面继续查找 k-- 64 // 即下次循环 mid = f[k-1-1]-1 65 k--; 66 } else if (key > temp[mid]) { // 我们应该继续向数组的后面查找(右边) 67 low = mid + 1; 68 // 为什么是k -=2 69 // 说明 70 // 1. 全部元素 = 前面的元素 + 后边元素 71 // 2. f[k] = f[k-1] + f[k-2] 72 // 3. 因为后面我们有f[k-2] 所以可以继续拆分 f[k-1] = f[k-3] + f[k-4] 73 // 4. 即在f[k-2] 的前面进行查找 k -=2 74 // 5. 即下次循环 mid = f[k - 1 - 2] - 1 75 k -= 2; 76 } else { // 找到 77 // 需要确定,返回的是哪个下标 78 if (mid <= high) { 79 return mid; 80 } else { 81 return high; 82 } 83 } 84 } 85 if(a[low]==key) { 86 return low; 87 } 88 else { 89 return -1; 90 } 91 } 92 }
原文:https://www.cnblogs.com/h--d/p/14892884.html