作者介绍了之前消除语言偏见模型,其主要分为两种:
前者需要大量的人工标注,并且最近的实验证明其精确度的提升仅仅来源于正则化的效果而不是恰当的视觉基础。后者则是通过一个纯问题的分支网络的训练进一步规范化模型,现有两种主要的方法:
作者认为,就算是比较小的损失,大量的累积起来一样会造成较大的损失,因此在进行消除语言偏见时应当重新平衡每个答案在总的VQA中,而不是简单的增加或减小每次的损失。
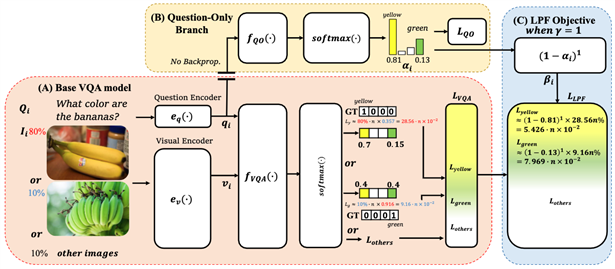
作者通过纯问题分支网络或得语言偏见,根据语言的偏见在主网络中为每个训练样本分配动态权重,实现消除语言偏见的效果
$$
L_{QO}=-\frac{1}{N}∑_{i=1}^{N}log?(softmax(f_{VQA}(v_i,q_i)))[a_i]
$$
作者将经过LSTM或GRU等的问题编码器生成的问题嵌入经过由MLP层组成的网络得到文本偏见。
损失函数如下:
$$
L_{QO}=-\frac{1}{N}∑_{i=1}^{N}log?(softmax(f_{QO}(q_i)))[a_i]
$$
根据人工标记真实的答案和纯问题模型的softmax层输出计算$$ a_i $$
$$
a_i=softmax(f_{QO}(q_i))[a_i]=\frac{exp(f_{QO}(q_i))[a_i]}{∑_{j=1}^{|A|}exp(f_{QO}(q_i))[a_j]}
$$
通过$$ a_i $$计算出形式化调制因子$$ \beta_i$$,其中$$ \gamma$$为超参数:
$$
\beta_i=(1-a_i)^\gamma,\gamma\geq0
$$
最后通过调制因子$$ \beta_i$$控制损失函数的权重:
$$
L_{LPF}=-\frac{1}{N}∑_{i=1}^{N}\beta_ilog(softmax(f_{VQA}(v_i,q_i)))[a_i]
$$
如下图所示,如果仅通过纯问题模型进行计算出来的答案,其$$ a_i$$比较大,因此其$$ \beta_i$$较小,使得其减小$$ L_{LPF}$$的权重。
LPF: A Language-Prior Feedback Objective Function forDe-biased Visual Question Answering
原文:https://www.cnblogs.com/boniii/p/14897076.html