度

• 结点拥有的子树数成为结点的度
• 树的度取树内各结点的度的最大值
• 度为0的结点称为叶结点（或终端结点）
• 度不为0的结点称为分支节点或非终端结点。分支节点称为内部节点。
• 树中结点的最大层次称为树的深度。

二叉树

二叉树特点

• 每个结点最多有两颗子树（即二叉树中不存在度大于2的结点）
• 左子树和右子树是有顺序的，次序不能颠倒（即使树中某结点只有一颗子树，也要区分它是左子树还是右子树）

五种基本形态

• 空二叉树
• 只有一个根结点
• 根结点只有左子树
• 根结点只有右子树
• 根结点既有左子树又有右子树

满二叉树的特点

• 叶子只能出现在最下一层
• 非叶子结点的度一定是2
• 在同样深度的二叉树中，满二叉树的结点个数一定最多，同时叶子也是最多

完全二叉树的特点

• 叶子结点只能出现在最下两层
• 最下层的叶子一定集中在左部连续位置
• 倒数第二层，若有叶子结点，一定都在右部连续位置
• 如果结点度为1，则该结点只有左孩子
• 同样结点数的二叉树，完全二叉树的深度最小

注：满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树

二叉树的性质

1. 在二叉树的第i层上至多有2^（i-1）个结点
2. 深度为k的二叉树至多有2^k-1个结点
3. 对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1
4. 具有n个结点的完全二叉树的深度为log2n(取下限)+1

二叉树的存储结构

顺序存储结构

用一维数组存储二叉树中的各个结点，并且结点的存储位置能体现结点之间的逻辑关系
弊端：对于一些特殊的二叉树（如斜树），会造成极大的浪费

链式存储结构（二叉链表）

二叉树每个结点最多有两个孩子，所以为它设计一个数据域和两个指针域，这样的链表叫做二叉链表

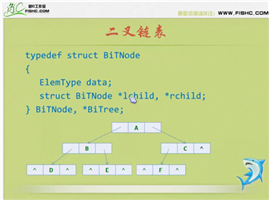
二叉树

原文：https://www.cnblogs.com/rfcaTheshy/p/14898907.html