动态规划的递推写法
一、数塔问题
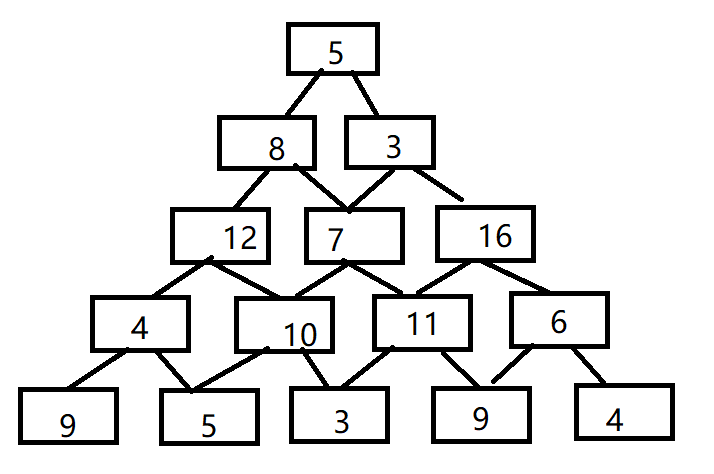
如图所示的一个数塔存储在一个二维数组中,f[i][j],其中i表示从上往下数的层数,j表示元素在这层从左往右数的位置,例如f[2][1]=8;现在从第一层向下走,每经过一个节点就把节点值累加,到达最后一层后返回,请问,在所有可能的遍历和中,能得到的最大值是多少。
如果尝试穷举所有可能的路径,可以观察发现,每个节点向下选择都有两种选择方式,如果把所有路径画出来刚好能画出一颗满二叉树
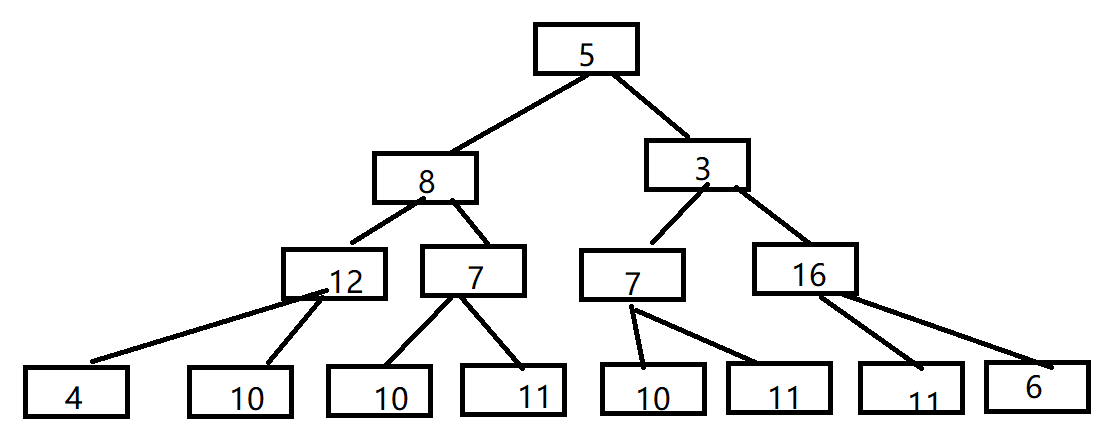
对这棵树从根节点到叶节点的所有路径就是数塔前四层可能的所有路径,很容易发现,在这颗树种有两颗完全相同的子树(节点7)。首先分析穷举法的时间复杂度,穷举法就是遍历整颗树的所有结点,然后每次遍历都有常数次加和操作(加和1次)。所以时间复杂度就是结点数O(2^n)。
既然这颗树中有重复子树,那么就可以采用动态规划的方法消去重复子树。其实就是求出7这颗子树所有可能路径的最大值,显然是18。那么再遍历相同子树的时候就可以直接取18这个值而不需要对子树进行遍历。
算法设计:核心思想就是记录下重复子树的“路径最大值”,所以可以申请一块大小为n的二维数组来记录值,那么就可是初始化一个二维数组dp[i][j],该下标表示第i行第j个元素的“路径最大值”。在计算“最大值时”应该从下往上计算,这样可以把路径最大值依次累加到上层结点上,累加到最后时顶层结点中存放的就是该数塔的路径最大值
归纳过程:求dp[1][1]=max(dp[2][1],dp[2][2])+f[1][1]
dp[2][1]=max(dp[3][1],dp[3][2])+f[2][1];dp[2][2]=max(dp[3][2],dp[3][3])+f[2][2]
归纳可得:dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+f[i][j]
代码:
1 #include <cstdio> 2 #include <algorithm> 3 using namespace std; 4 const int maxn = 1000; 5 int f[maxn][maxn],dp[maxn][maxn]; 6 int main(){ 7 int n; 8 scanf("%d",&n); 9 for(int i=1;i<=n;i++){ 10 for(int j=1;j<=i;j++){ 11 scanf("%d",&f[i][j]); 12 } 13 } 14 for(int j=1;j<=n;j++){ 15 dp[n][j] = f[n][j];//先把最后一层的值初始化给dp,用于计算上一次的值 16 } 17 for(int i=n-1;i>=1;i--){ 18 for(int j=1;j<=i;j++){ 19 dp[i][j] = max(dp[i+1][j],dp[i+1][j+1])+f[i][j]; 20 } 21 } 22 printf("%d\n",dp[1][1]); 23 return 0; 24 }
个人愚见:关于该程序的递归实现,我认为有可能实现,因为根据算法可以画出递归树,那么递归应该是可以实现的,但是就实现难度上来说,由于本人能力有限,还是很难想象实现方式,因为要对二维数组进行操作,而递归函数又需要用到数组下标,但是只能返回一个结果,那这样的效率还不如递推实现方式。如果有读者了解递归方法欢迎评论区留言。
二、动态规划的比较
动态规划和分治算法:显然动态规划和分治都是通过将一个复杂问题分解然后逐步求解最后合并的思想,但是区别在于,动态规划中划分出的子问题的有重叠问题的,二分治法划分出的子问题都没有重叠问题,就像快排和归并排序那样。
动态规划和贪心算法:动态规划和贪心算法都在寻找一个最优解的子问题,但是区别在于,贪心是一种只针对当前情况的选择,不会考虑以后的结果是否是最优,而动态规划是通过一堆子问题的合并,然后选择当前所有可选子问题答案中的最优解。或者说,贪心算法只顾眼前,不顾以后;而动态规划算法考虑了在后续选择中的情况。这点可以结合分治来一起理解,因为动态规划是通过把一堆子问题结合而出现的最优解选择,也就是从少到多一步一步累计上来的,而贪心没有进行问题的划分,自然不存在对最优子问题的分析。
原文:https://www.cnblogs.com/zyq79434/p/14915594.html