设 为数集，
为双射，则对每个
都有唯一确定的
满足
（即这样与之对应）。按照映射的定义，这就定义了一个映射（记为）
，称为是
的反函数，其表达形式为
。
注1：定义反函数的前提是，原函数是双射（一对一）。同济版高数中，反函数的定义是“设 为单射，......”因为是到
那肯定是满射，所以也等同于要求是双射。
另外，关于反函数的双射要求
定义中要求的双射，就是一对一，左边右边都没有多余的没用上的点。
因为这样的定义，最简洁，也足够应付各种反函数的应用场景。
其实，扩展到一对一，左边或右边有多余的没用上的点，虽然也没有矛盾之处，但既然它们是多余的没有用上的，从数学追求简洁的角度，干脆不带着它们就好了。
这在函数定义时，也是一样的道理。对每一个x属于D，就是把D中元都用上，不用的多余的点也没有必要带着它们。
注2：定义域和值域发生互换：原函数的值域是反函数的定义域，原函数的定义域是反函数的值域。
注3：从几何图形来看，原函数与反函数的曲线关于直线 是对称的。
注4：关系式 成立，即二者的复合是恒等映射：
。应用（一种常用变形）：
.
函数（映射）允许“多对一”，如 ，但不允许“一对多”。这实际上可以用
竖直线检验：任何一条竖直直线与函数曲线至多有一个交点。
例如， ，移动竖直直线都只有一个交点：
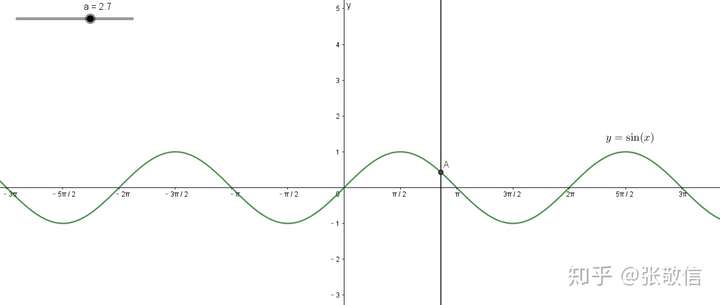
对于一个函数，再考虑其是否有反函数，只需要再保证”不能多对一“即可。这可以用：
水平线检验：任何一条水平直线与函数曲线至多有一个交点。
注意，函数是否存在反函数与所考察的区间是有关系的，例如， 在整个
上来看，是不满足水平线检验的：
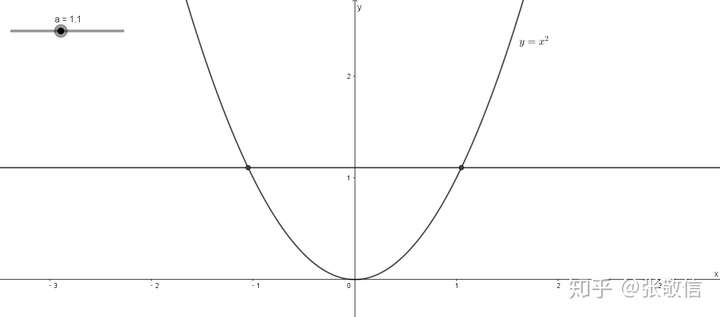
但是，如果只考虑 或者
，就满足水平线检验，就存在反函数了。
类似的，还有三角函数，比如 ，在多个周期内，显然是不满足水平线检验的，但在一个单调周期内，如
是满足水平线检验的，因此
在
上有反函数，
那么，在 也是有反函数的，这么多单调周期都可以选择，但当然是选更简单的包含原点周期更好。
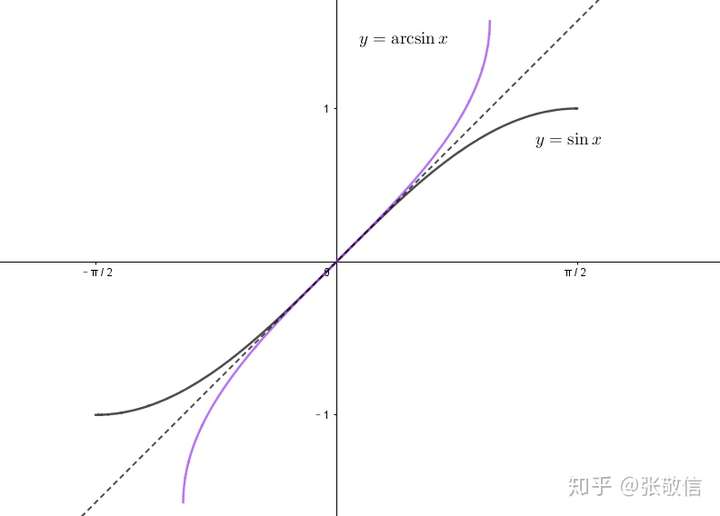sin(x)选择的是[-π/2, π/2]单调周期
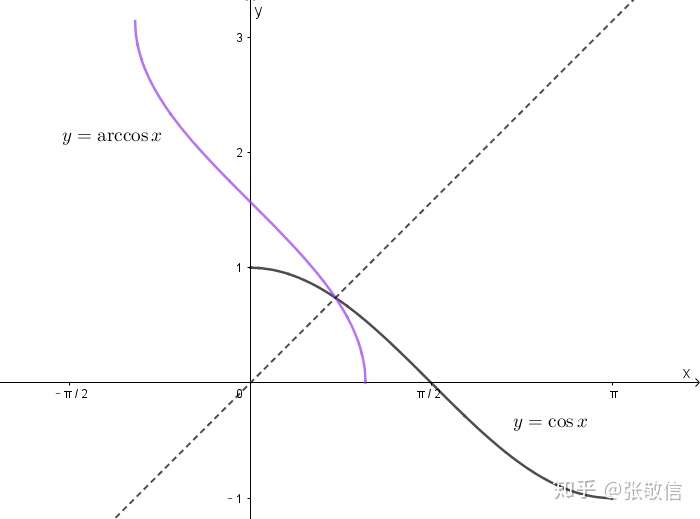cos(x)选择的是[0, π]单调周期
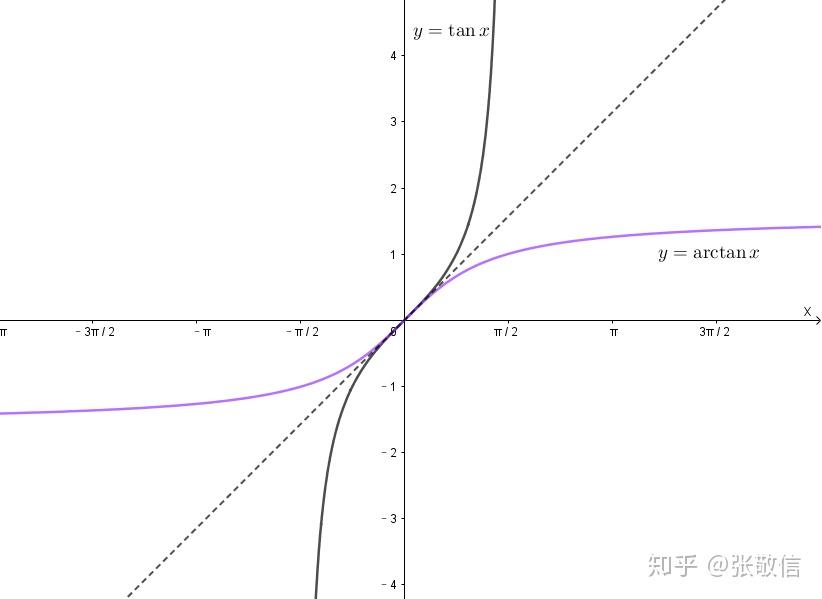tan(x)选择的是[-π/2, π/2]单调周期
可见，三角函数的反函数一般是选择包含原点或从原点开始的单调周期。
(1) 检验函数是否为双射，或者做水平线检验，确定反函数存在性；表示原函数的定义域，注意，可能需要限制在部分单调区间。
(2) 根据 反解出
, 注意从求解过程的一些限制（如分母不为
, 根号下大于等于
等）得到反函数的定义域。
(3) 换表示，即交换 和
，得到最终的反函数。
注：反函数一般是在原函数的单调区间才存在的，也可以借助函数图形、函数单调性、定义域与值域是互换关系，来得到反函数的定义域加以验证。
例1 设 , 求反函数
.
解：(1) 画出函数图形，做水平线检验：
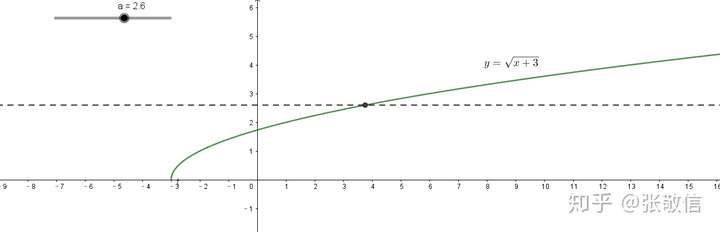
至多有一个交点，故存在反函数。
(2) 原函数是 ，
注意开根号是 ，故有
解出 :
(3) 换表示，得到反函数为：
最后再绘制原函数与反函数的图像看看，
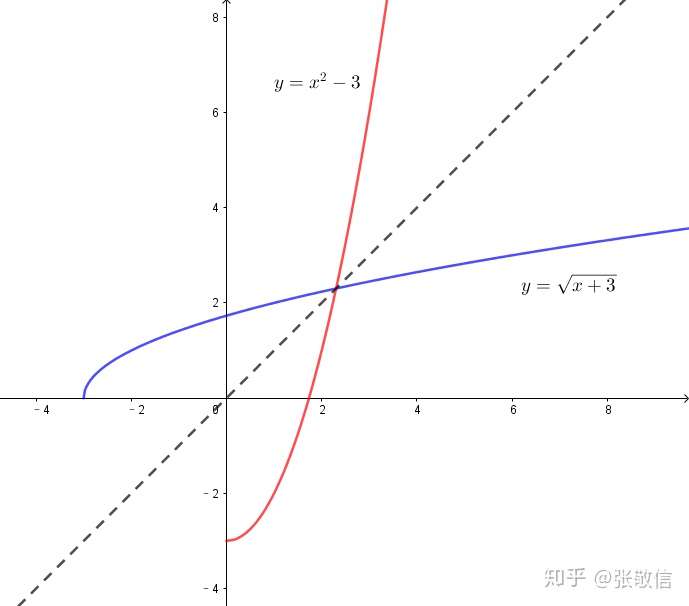
注：绘制原函数与反函数图形时有一个技巧，比如上例，通过绘制两个参数方程函数来实现：
，
，
Geogebra绘图命令：
曲线((t, sqrt(t + 3)), t, -3, 10)
曲线((sqrt(t + 3), t), t, -3, 10)
x
例2 设 , 求反函数
.
解：(1) 画出函数图形，满足水平线检验：
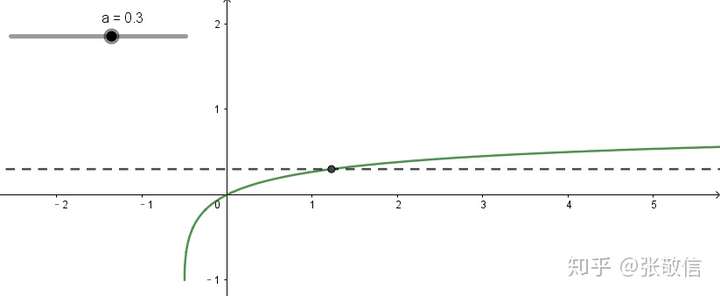
故存在反函数。
(2) 原函数是 ，
解出 :
注意，作为根号部分，应有 ，可推得
又分母不能为 ，故
, 从而
继续求解 :
(3) 换表示，得到反函数：
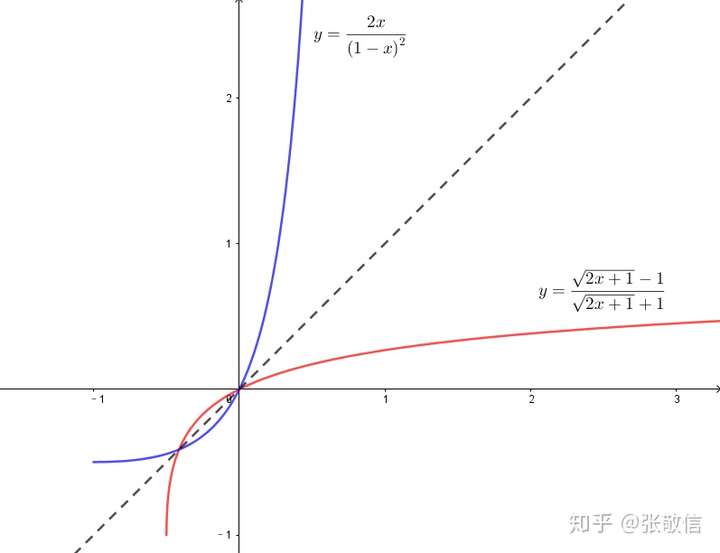
最后再绘制原函数与反函数的图像看看，
——————————————————————
补充：关于反函数，有同学还是没绕明白
其实真正理解了，就不会绕了。
函数的三要素有：定义域，对应法则，值域。前两个是根本，他俩决定了值域。
函数本质上是，数集与数集的(非一对多的)对应关系，其表达式用哪个符号表示并不重要，重要的定义域和对应法则所决定的这种对应关系。
为了简单，把反函数定义限制为首先得是双射(一对一的)。
原函数 ，反函数就是
，且保持对应关系不变。
举个例子，
原函数 ，对应法则表达形式为
按标准步骤求，或者直接取反对应关系(因为简单能直接看出来)，
反函数 ，对应法则表达形式为
以上是正确解答。
————————————————分割线————————————————
有个同学说了，上面原函数 的反函数，不能交换一下是
吗？(正着
是
的
倍，反过来
是
的
倍)
咱们来看看，为什么不对。
首先只说表达式，不说定义域，这不完整（他的困扰和没绕明白，恰恰就是不说定义域造成的）。
(1) 假如说，你这个反函数是
显然不对，因为这个函数把， 对应到
，
对应到
，
对应到
，根本就回不去
了。
(2) 假如说，你这个反函数是
你这不就是原来的原函数，换了个名字吗？(定义域相同，对应法则相同)它还是原函数。
原文：https://www.cnblogs.com/lucas-liang/p/14927281.html