一元多项式的计算
当表达式为p0 + p1x^1 + p2x^2 + p3x^3 + ····pn*x^n;
可以使用以为数组来表示
Pn(x)
| 0 | 1 | 2 | 3 | n |
|---|---|---|---|---|
| p0 | p1 | p2 | p3 | pn |
Qn(x)
| 0 | 1 | 2 | 3 | n |
|---|---|---|---|---|
| q0 | q1 | q2 | q3 | qn |
则线性表Rn(x) = Pn(x) + Qn(x) 为
| 0 | 1 | 2 | 3 | n |
|---|---|---|---|---|
| p0+q0 | p1+q1 | p2+q2 | p3+q3 | pn+qn |
当我们遇见系数多项式的时候
S(x) = 1 + 3X10000+2X20000
这时候在使用上面的的方法未免有点太浪费空间了
所以我们应只是记录系数不为零的项
| 0 | 1 | 2 |
|---|---|---|
| 1 | 3 | 2 |
| 0 | 10000 | 20000 |
第二行表示多项式的系数
第三行表示多项式的指数
线性表 A = ((7,0),(3,1),(9,8),(5,17))
线性表 B = ((8,1),(22,7),(-9,8))
创建一个数组c
分别从头遍历比较a和b的每一项
指数相同,对应系数相加,若其和不为零,则在c中增加一个新项
指数不同,则将指数较小的项复制到c中
当一个多项式遍历完毕后,将另一个剩余的项依次复制到c中即可
顺序存储结构存在的问题
存储空间分配不灵活
运算的空间复杂度高
解决方法: 采用链式存储结构,动态分配内存
定义
ADT liet
{
? 数据对象:D = {ai | ai 属于Elemset,(i = 1,2,3,····n,n>=0)}
? 数据关系:R = {<ai-1, ai>| ai-1, ai属于D(i = 1,2,····,n)}
? 基本操作:
? initlist(&l);
? DestroyList(&l);
? ClearList(&l);
? ListEmpty(L);
}ADT list
initlist(&l)
? 操作结果:构造一个空的线性表
DestroyList(&l)
? 初始条件:线性表L已经存在
? 操作结果:销毁线性表L;
ClearList(&l)
? 初始条件:线性表L已经存在
? 操作结果:将线性表L重置为空表
ListEmpty(L)
? 初始条件:线性表L已经存在。
? 操作结果: 若线性表L为空表,则返回True,否则返回False
第二周第八节
#define LIST_LENGTH 100
typedef struct
{
int realpart;
int imagpart;
}ElemType;
typedef struct
{
ElemType elem[LIST_LENGTH];
int length;
}Sqlist;
typedef struct
{
ElemType *data;
int length;
}Sqlist;
Sqlist L;
L.data = (ElemType*)malloc(sizeof(Elemtype)*MaxSize);
#include <stdio.h>
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
// Status 是函数的类型,其值是函数结果状态代码
typedef int Status;
typedef char ElemType;
// 线性表的初始化
Status InitList_Sq(SqList &L)
{
L.elem = new ElemType[MAXSIZE];
if(!L.elem)exit(OVERFLOW);
L.lengh = 0;
return OK;
}
// 销毁
void DsetroyList(SqList &L)
{
if(L.elem)
delete L.elem; // 释放空间
}
// 清空线性表L
void ClearList(SqList &L)
{
L.length = 0; // 将线性表的长度置为零
}
// 得到i位置上的元素
int GetElem(SqList L, int i, ElemType &e)
{
// 判断i的值是否合理,若不合理,返回ERROR
if(i < 1 || i < L.length)
return ERROR;
e = L.elem[i-1];
return OK;
}
顺序查找法:
? 将表中元素进行遍历,依次比较如果查找出来则返回对应的记录, 如果没找到则返回0;
? 例如一个长度为7的数组进行查找,最少找一次,最多找7次,那么平均一共找4次即可。
平均查找长度ASL(Average Search Length)
对含有n个记录的表,查找成功时:
? ASL = (i从1到n加)PiCi = (n+1)/2;
? Pi第i个记录被查找的概率
? Ci找到第i个记录需要比较的次数
? 例如上面的长度为7的数组查找到平均长度为1/7乘1 + 1/7乘2 + ····1/7乘7 每一个的查找的概率都是1/7, 只是查找到需要的次数不同。
插入位置在最后:这接放在最后即可
插入位置在中间:让别插入的位置的后面的元素依次向后移
插入位置在最前面: 让所有位置依次往后移,给这个位置移出来地方
算法思想
插入位置的判断(0-数组长度)
判断顺序表的存储空间是否已满,若已经满了则返回ERROR
将第n至i为的元素依次向后移动一个位置,空出第i个位置
将要插入的新元素e放入第i个位置
表长加一
Status ListInsert_Sq(SqList &L, int i,ElemType e)
{
if( i < 1 || i > L.length + 1)return ERROR;
if(L.length == MAXSIZE) return ERROR;
for(j = L.length-1; j >= i-1; j--)
{
L.elem[j+1] = L.elem[j];
}
L.elem[i-1] = e;
L.length++;
return OK;
}
时间分析
若插入在为节点则无需移动(特别快)
若插入在首节点。则表中元素都向后移(特别慢)
若要考虑在各种位置插入(共n+1种情况)
E(ins) = 1/(n+1)(从1到n+1)[n-i+1] = 1/(n+1) *(0+1+2+3+·····n) = 1/(n+1) * n(n+1)/2 = n/2;
时间复杂度O(n);
Status ListDelete_Sq(SqList &L, int i, int e)
{
if((i<1)||(i>L.length))return ERROR;
e = L.elem[i-1];
for(j = i;j <=L.length-1; j++)
L.elem[j-1] = L.elem[j];
L.length--;
return e;
}
时间消耗分析
| i=1 | i=2 | i=3 | ···· | i = n |
|---|---|---|---|---|
| n-1 | n-2 | n-3 | ···· | 0 |
E(del) = 1/n (i从1到n)(n-i) = 1/n * (n-1)*n/2 = (n-1)/2;
时间复杂度为O(n);
使用new来代替c语言中malloc的臃长代码
new 类型名T(初始值表)
? 功能: 申请用于存放T类型对象的内存空间,并依初值列表来赋初值
? 结果值:
? 成功:T类型的指针,指向新分配的内存
? 失败: 0(NULL)
delete 指针p
功能:
? 释放指针p所指向的内存,p必须是new操作的返回值
函数调用时传送给形参表的实参必须是形参三个一致
? 类型,个数,顺序
参数传递时有两种方式
传值方式:参数为整型,实型,字符型等;
传地址
参数为指针变量
参数为引用类型
这个是c++中的语法
void main()
{
int i = 5;
int &j = i;
i = 7;
}
则j也等于7; 其中第二个步骤的含义就是j 是 i 的别名,他们俩是同一个东西,改一动二
// 第一种
int main()
{
float a,b;
swap(&a,&b);
}
void swap(float *m, float *n)
{
float temp;
temp = *m;
*m = *n;
*n = temp;
}
// 第二种 c++方法
int main()
{
float a,b;
swap(a,b);
}
// 这里就是交换ab的值, 使用c++中的语法 & 来给a,b取别名,从而交换mn的值来交换ab的值
void swap(float &m, float &n)
{
float temp;
temp = m;
m = n;
n = temp;
}
参数为数组名
引用类型做形参的三点说明
单链表
双链表
循环链表
头指针,头结点,首元节点
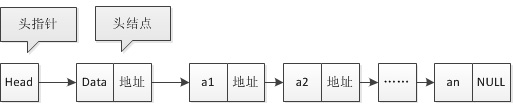
链表的两种形式
带头结点的

不带头结点的

讨论:在链表中设置头结点有什么好处
便于首元节点的处理
首元节点的地址保存在头结点的指针域中,所以在链表中第一个位置操作和其他位置相同,无需进行任何处理
便于空表和非空表的统一处理
无论链表是否为空,头指针都是指向头结点的非空指针,因此空表和非空表的处理也就同一了
讨论:头结点的数据域内装的是什么
? 头结点的数据域可以为空,可以存放表的长度等附加信息,但是此节点不能计入链表长度值
如何表示空表
链表的特点
单链表的命名
单链表基本操作的实现
单链表的初始化
算法步骤
算法描述
// 初始化
Status LnitList_L(LinkList &L)
{
L = new LNode; // 或者 L = (LNode*)malloc(sizeof(LNode));
L->next = NULL;
return OK;
}
补充算法------判断链表是否为空
空表: 链表中无元素,称为空链表(头指针和头结点仍然存在)
算法思路:判断头结点的指针域是否为空
int ListEmpty(LinkList L)
{
if(L->next)
return 0;
else
return 1;
}
补充算法-------单链表的销毁,链表销毁后不存在(头结点,头指针都不存在)
算法思路:从头指针开始,依次释放所有的结点,这里需要有两个指针变量,一个指向头结点,另一个指向头结点的下一个
循环结束条件 头指针为空
Status DeleteList_L(LinkList *L)//销毁单链表L
{
Londe *p;
p = (LNode*)malloc(sizeof(LNode));
while(L)//循环结束条件L不为空
{
p = L;//先将头结点地址赋值给临时变量
L = L->next;//再将头指针指向下一个
free(p);//释放该节点
}
return OK;
}
补充算法 ------ 清空链表
链表仍然存在,但链表中无元素,成为空链表(头结点,头指针依然存在)
算法思路,依次释放所有结点,并将头结点指针域设置成空
循环结束条件 指向最后一个元素
Status ClearList_L(LinkList *L)//清空单链表L
{
Londe *p,*q;
p = L->next;
while(p)//循环结束条件指向最后一个了
{
q = p->next;
free(p);//释放该节点
p = q;
}
L->next == NULL;
return OK;
}
补充算法 ---- 求单链表的表长
思路:从首元节点开始,依次计数所有结点
int ListLength_L(LinkList L) // 返回值中数据元素的个数
{
int i = 0;
LNode *p;
p = L->next;
while(p)
{
i++;
p = p->next;
}
return i;
}
取值-----取单链表中第i个元素的内容
思路:从链表的头指针出发顺着链域next逐个结点往下搜索,知道索搜到第i个结点为止,因此,链表不是随机存取结构
步骤:
从第一个结点(L->next)顺链扫描用指针p记录当前所扫描到的结点,p的初值为p=L->next
.j做计数器,累计当前扫描过的节点数,j的初值为1
当p指向扫描到的下一节点的时候,计数器j+1
当j === i时找到,退出程序
Status GetElem_L(LinkList L, int i, ElemType &e)
// 获取线性表中的某个数据元素,通过变量e返回
{
p = L->next;
while(p&&j<i)
{
p = p->next;
j++;
}
if( j == i)
{
e = p->data
}
else
{
return ERROR;
}
}
查找:
插入:在第i个结点前插入新结点
Lnode *LocateElem_L(LinkList L, Elemtype e)
// 在线性表中查找值为e的数据元素
// 找到,则返回L中值为e的数据元素的地址,查找失败返回NULL
{
LinkList p;
p = L->next;
while(p&&p->data!=e)
{
p = p->next;
}
// 返回地址
return p;
}
Lnode *LocateElem_L(LinkList L, Elemtype e)
// 在线性表中查找值为e的数据元素
// 找到,则返回L中值为e的数据元素的位置,查找失败返回NULL
{
int i = 1;
LinkList p;
p = L->next;
while(p&&p->data!=e)
{
p = p->next;
i++
}
// 返回地址
if( p!=NULL)
{
return i;
}
else
{
return 0;
}
}
插入:在第i个结点前插入新节点
Status ListInsert_L(LinkList &L, int i, Elemtype e)
// 在L中第i个元素之前插入数据元素e
{
int a = 0;
LinkList p, q;
p = L;
while(a < i-1 && p)
{
p = p->next;
a++;
}
if( a == i-1 )
{
q = (LNode*)malloc(sizeof(LNode))
q->data = e;
p->next = q->next;
p->next = q;
// 这两步交换位置的算法不能颠倒先后位置,否则会导致,数据丢失,交换失败
return OK;
}
else
{
return ERROR
}
}
删除 删除第i个结点
Status ListDelete_L(LinkList &L, int i, Elemptype &e)
// 在L中删除第i个元素
{
int a = 0;
LinkList p, q;
p = L;
while(p->next && a <i-1)
{
p=p->next;
a++;
}
if( !(p->next) || a >i-1)
return ERROR;
q = p->next;
e = q->data;//保存要删除的元素的位置
p->next = q->next;
free(q);
return OK;
}
原文:https://www.cnblogs.com/nuli-fendou/p/14948302.html