异面直线所成的角

前言

两条共面直线所成的角的范围是： \([0，\cfrac{\pi}{2}]\) ，两条异面直线所成的角的范围是 \((0，\cfrac{\pi}{2}]\) .

求解思路

典例剖析

【2021年高考乙卷文数第\(10\)题理数第\(5\)题】 在正方体 \(ABCD-A_{1}B_{1}C_{1}D_{1}\) 中， \(P\) 为 \(B_{1}D_{1}\) 的中点， 则直线 \(PB\) 与 \(AD_{1}\) 所成的角为 【\(\quad\)】

解析: 由于 \(AD_{1}//BC_{1}\)， 所以 \(\angle PBC_{1}\) 是直线 \(PB\) 与 \(AD_{1}\) 所成的角[或所成角的补角]准确的说法还需要添加这句话，或所成角的补角，原因是两条直线所成的角的范围是 \([0,\cfrac{\pi}{2}]\) ，而图形中的角 \(\angle PBC_{1}\) 的大小不一定在此范围内，

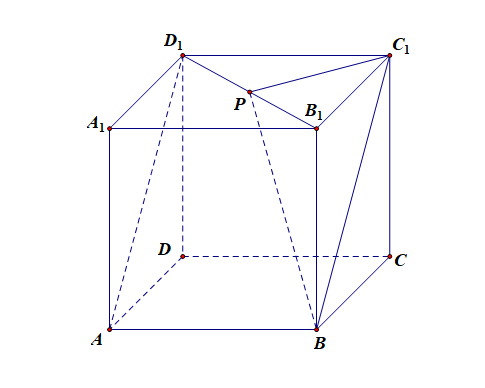
设正方体 \(ABCD-A_{1}B_{1}C_{1}D_{1}\) 的棱长为 \(2\)，

则 \(PB_{1}=PC_{1}=\cfrac{1}{2}\sqrt{2^{2}+2^{2}}=\sqrt{2}\)，

\(BC_{1}=\sqrt{2^{2}+2^{2}}=2\sqrt{2}\)， \(BP=\sqrt{2^{2}+(\sqrt{2})^{2}}=\sqrt{6}\)，

所以 \(\cos\angle PBC_{1}=\cfrac{PB^{2}+BC_{1}^{2}-PC_{1}^{2}}{2\times PB\times BC_{1}}=\cfrac{6+8-2}{2\times\sqrt{6}\times2\sqrt{2}}=\cfrac{\sqrt{3}}{2}\)，

所以，\(\angle PBC_{1}=\cfrac{\pi}{6}\)， 则直线 \(PB\) 与 \(AD_{1}\) 所成的角为 \(\cfrac{\pi}{6}\)， 故选: \(D\) .

异面直线所成的角

原文：https://www.cnblogs.com/wanghai0666/p/14962356.html