动态规划：背包问题

01 背包

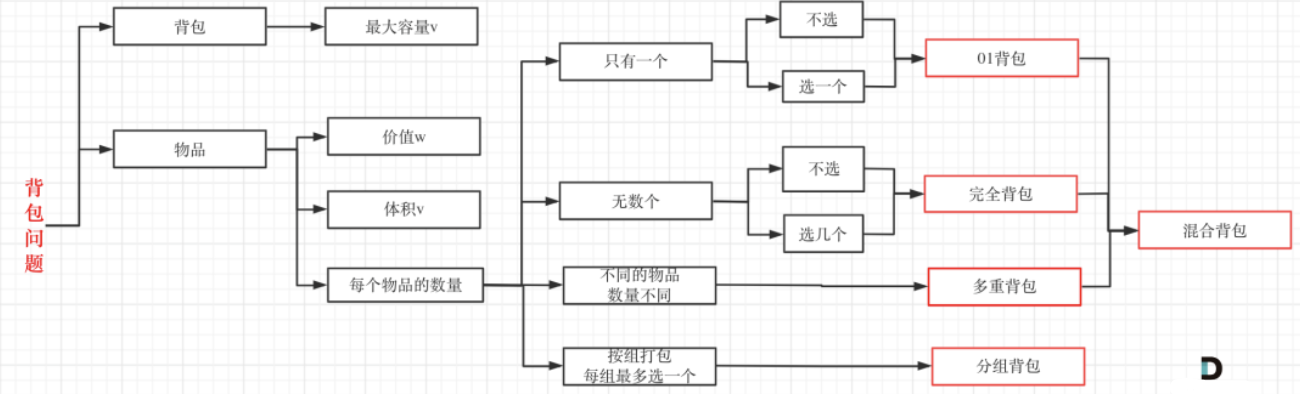
背包问题的理论基础是01背包。

有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

例子：
背包最大重量为4。

问背包能背的物品最大价值是多少？

动规五部曲

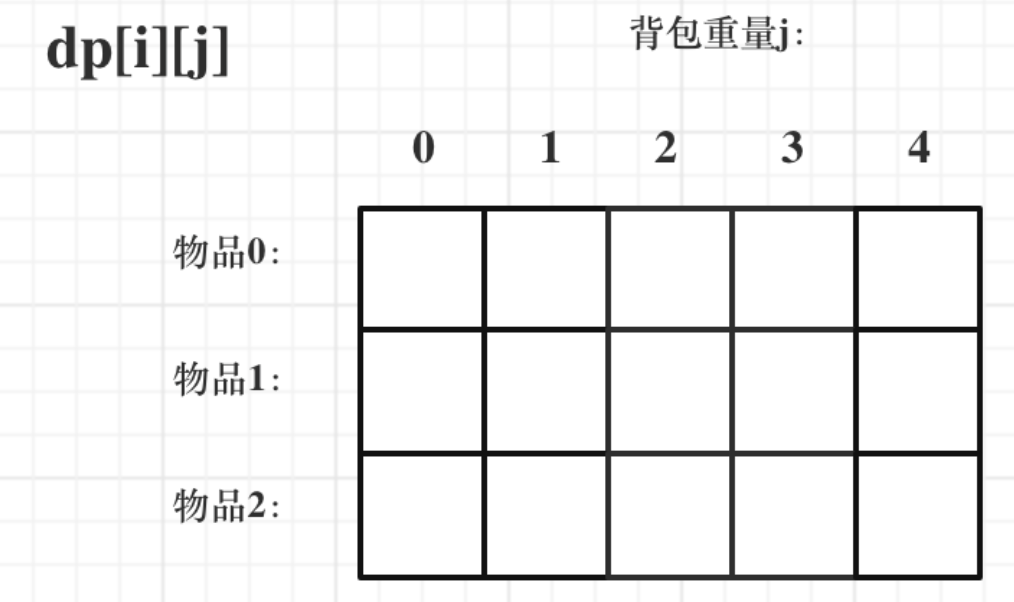
1. 确定dp数组以及下标的含义
   对于背包问题是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
   

2. 确定递推公式
   可以有两个方向推出来dp[i][j]，

   • 由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]
   • 由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
     所以递归公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

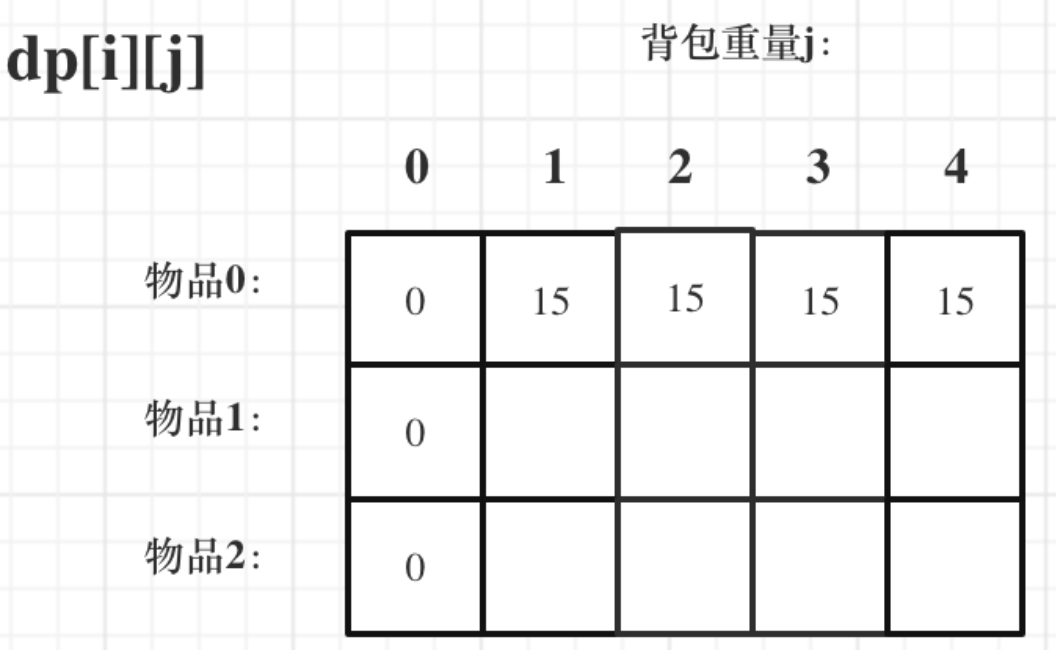
3. dp数组如何初始化
   首先如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。
   由状态转移方程可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。dp[0][j]为存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

// 初始化需要倒叙遍历，如果一旦正序遍历了，那么物品0就会被重复加入多次
for (int j = bagWeight; j >= weight[0]; j--) {
    dp[0][j] = dp[0][j - weight[0]] + value[0]; // 初始化i为0时候的情况
}

4. 确定遍历顺序
   有两个遍历的维度：物品与背包重量。两者哪个先遍历其实都可以，但是先遍历物品更好理解。

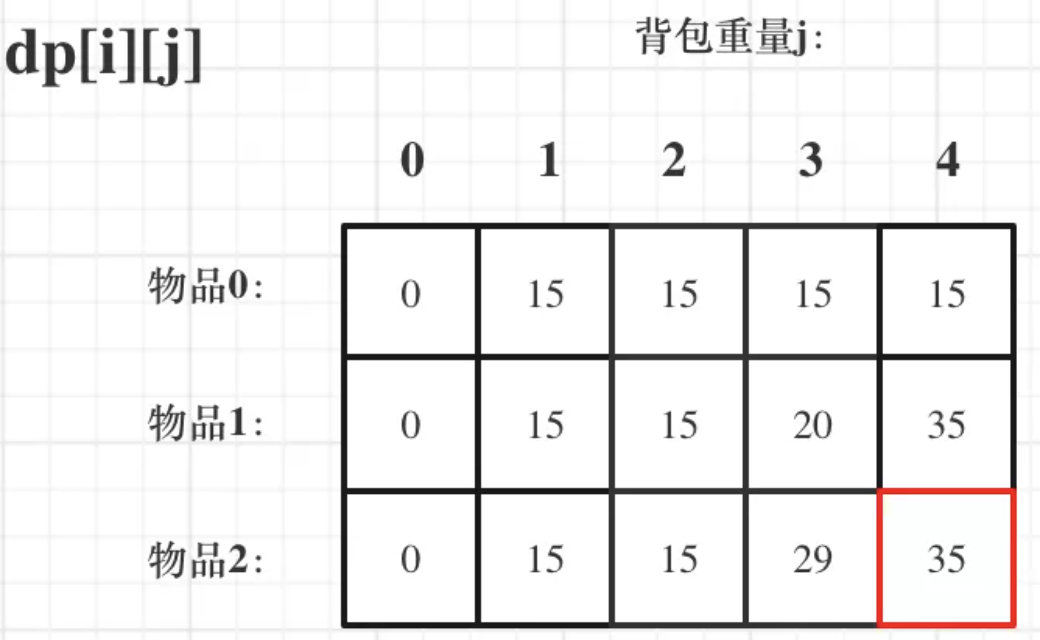
先遍历物品，然后遍历背包重量：

// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 
        if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 这个是为了展现dp数组里元素的变化
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        
    }
}

先遍历背包，再遍历物品:

// weight数组的大小 就是物品个数
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

5. 举例推导dp数组
   来看一下对应的dp数组的数值，如图：
   

代码

    public static void main(String[] args){
        int[] weight = {1, 3, 4};
        int[] value = {15, 20, 30};
        int bagWeight = 4;

        // 二维数组
        int[][] dp = new int[weight.length][bagWeight + 1];

        // 初始化
        for (int j = bagWeight; j >= weight[0]; j--) {
            dp[0][j] = dp[0][j - weight[0]] + value[0];
        }

        // weight数组的大小 就是物品个数
        for(int i = 1; i < weight.length; i++) { // 遍历物品
            for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
                if (j < weight[i]) dp[i][j] = dp[i - 1][j];
                else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

            }
        }

        System.out.println(dp[weight.length - 1][bagWeight]);
    }

动态规划：背包问题

原文：https://www.cnblogs.com/luedong/p/14964762.html