题目描述

题目源自于42. Trapping Rain Water

给定n个非负整数，代表着一个高度柱状图连续n个图的高度。本题需要计算这个柱状图能够蓄水的数量。

解题思路

蓄水的情况主要如下图：

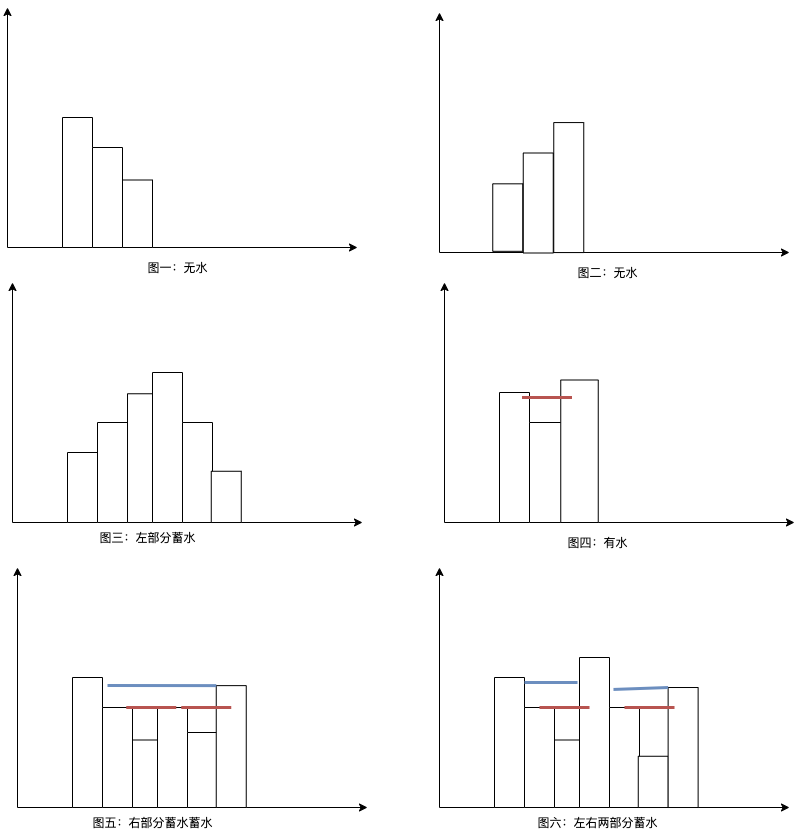
假设heights代表所有的柱状图高度， heights[i](0<=i<len(heights))代表第i个柱状图的高度：

根据上图一、图二和图三可知：

1. 当任意heights数值呈单调的时候，不存在蓄水量。
2. 当heights仅存在类正态曲线的分布时，不存在蓄水量。

笔者先将情况缩小为len(heights) == 3，结合图四可知：

1. 当heights[i] < heights[i+1] and heights[i] < heights[i-1]时存在蓄水量。
2. 当前可以蓄水，蓄水量为(min(heights[i], heights[i-1]) - heights[i])
3. 此时相当于heights[i] = min(heights[i], heights[i-1])

接下将场景扩大下len(heights) > 3，可参见图五和图六：

假设当前的bar的下标为k，检查蓄水的bar下标为i(i<k)，此时任意j(i<j<k)都有heights[i] < heights[j] < heights[j+1] < heights[k]：

1. 当heights[i-1] > heights[i]时存在蓄水量，执行2，否则执行5。
2. 蓄水量相当于(min(min(heights[i+1:k+1]), heights[i-1]) - heights[i]) * (k-i)。
3. 此时相当于heights[i] = min(min(heights[i+1:k+1]), heights[i-1])。
4. i=i-1，执行步骤1。
5. k=k+1,i=k-1执行步骤1。

根据上述步骤可以一步步获得最终的结果，得算法如下：

class Solution:
    def trap(self, height: List[int]) -> int:
        water = 0
        hi = 2
        while hi < len(height):
            if height[hi] < height[hi-1]:
                hi+=1
                continue
            bar = self._get_last_bar(height, hi-1, height[hi])
            while bar is not None:
                for i in range(hi-1, bar-1, -1):
                    water += min(height[hi], height[bar-1]) - height[i]
                    height[i] = min(height[hi], height[bar-1])
                bar = self._get_last_bar(height, bar-1, height[hi])
            hi+=1
        
        return water
    
    def _get_last_bar(self, height, lo, mh):
        if lo - 1 < 0:
            return None
        while lo - 1 >= 0 :
            if height[lo] < min(height[lo-1], mh):
                return lo
            lo-=1
        return None

上述算法实际上是O(n^2)，算法还存在比较多得优化空间：

1. 如使用栈来减少回朔(O(n))：https://leetcode.com/problems/trapping-rain-water/discuss/17414/A-stack-based-solution-for-reference-inspired-by-Histogram
2. 使用双指针遍历法(O(n))：https://leetcode.com/problems/trapping-rain-water/discuss/17554/Share-my-one-pass-Python-solution-with-explaination

相关题目：

• 11. Container With Most Water

LeetCode：Trapping Rain Water

原文：https://www.cnblogs.com/kulor/p/14979616.html