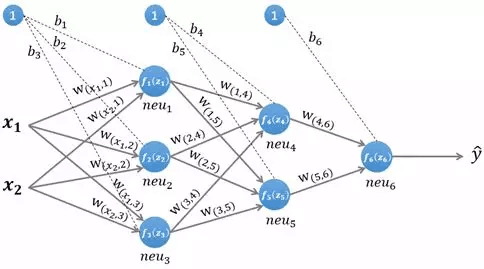
图1 一个简单的三层神经网络
图1所示是一个简单的三层(两个隐藏层,一个输出层)神经网络结构,假设我们使用这个神经网络来解决二分类问题,我们给这个网络一个输入样本,通过前向运算得到输出。输出值的值域为,例如的值越接近0,代表该样本是“0”类的可能性越大,反之是“1”类的可能性大。
为了便于理解后续的内容,我们需要先搞清楚前向传播的计算过程,以图1所示的内容为例:
输入的样本为:
${\Large \overrightarrow{\mathrm{x}}=\left(x_{1}, x_{2}\right)^{T}} $
第一层网络的参数为:
${\Large W^{(1)}=\left[\begin{array}{l} w_{\left(x_{1}, 1\right)}, w_{\left(x_{2}, 1\right)} \\ w_{\left(x_{1}, 2\right)}, w_{\left(x_{2}, 2\right)} \\ w_{\left(x_{1}, 3\right)}, w_{\left(x_{2}, 3\right)} \end{array}\right], \quad b^{(1)}=\left[b_{1}, b_{2}, b_{3}\right]} $
第二层网络的参数为:
${\Large W^{(2)}=\left[\begin{array}{l} w_{(1,4)}, w_{(2,4)}, w_{(3,4)} \\ w_{(1,5)}, w_{(2,5)}, w_{(3,5)} \end{array}\right], \quad b^{(2)}=\left[b_{4}, b_{5}\right]} $
第三层网络的参数为:
${\Large W^{(3)}=\left[w_{(4,6)}, w_{(5,6)}\right], \quad b^{(3)}=\left[b_{6}\right]} $
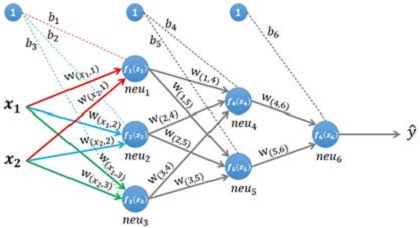
图2 计算第一层隐藏层
第一层隐藏层有三个神经元:neu1、neu2 和 neu3。该层的输入为:
${\large z^{(1)}=W^{(1)} *(\vec{x})^{T}+\left(b^{(1)}\right)^{T}} $
神经元 neu1的输入:
${\Large z_{1}=w_{\left(x_{1}, 1\right)} * x_{1}+w_{\left(x_{2}, 1\right)} * x_{2}+b_{1}} $
神经元neu2的输入:
${\Large z_{2}=w_{\left(x_{1}, 2\right)} * x_{1}+w_{\left(x_{2}, 2\right)} * x_{2}+b_{2}} $
神经元neu2的输入:
${\Large z_{3}=w_{\left(x_{1}, 3\right)} * x_{1}+w_{\left(x_{2}, 3\right)} * x_{2}+b_{3}} $
假设我们选择函数f(x)作为该层的激活函数(图1中的激活函数都标了一个下标,一般情况下,同一层的激活函数都是一样的,不同层可以选择不同的激活函数),那么该层的输出为:$f_{1}\left(z_{1}\right)$ 、 $f_{2}\left(z_{2}\right) $ 和 $ f_{3}\left(z_{3}\right) $。
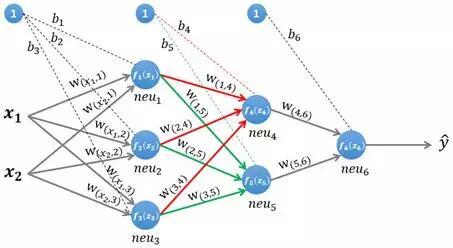
图3 计算第二层隐藏层
第二层隐藏层有两个神经元:neu4 和 neu5。该层的输入为:
${\large { \mathbf{z}^{(2)}=\boldsymbol{W}^{(2)} *\left[f_{1}\left(z_{1}\right), f_{2}\left(z_{2}\right), f_{3}\left(z_{3}\right)\right]^{T}+\left(\boldsymbol{b}^{(2)}\right)^{T}} } $
即第二层的输入是第一层的输出乘以第二层的权重,再加上第二层的偏置。因此得到 neu4 和 neu5 的输入分别为:
${\Large z_{4}=w_{(1,4)} * f_{1}\left(z_{1}\right)+w_{(2,4)} * f_{2}\left(z_{2}\right)+w_{(3,4)} * f_{3}\left(z_{3}\right)+b_{4}} $
${\Large z_{5}=w_{(1,5)} * f_{1}\left(z_{1}\right)+w_{(2,5)} * f_{2}\left(z_{2}\right)+w_{(3,5)} * f_{3}\left(z_{3}\right)+b_{5}} $
该层的输出分别为:$f_{4}\left(z_{4}\right)$ 和$f_{5}\left(z_{5}\right)$。
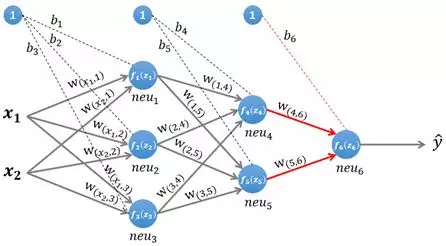
图4 计算输出层
输出层只有一个神经元:neu6。该层的输入为:
${\large \mathbf{z}^{(3)}=\boldsymbol{W}^{(3)} *\left[f_{4}\left(z_{4}\right), f_{5}\left(z_{5}\right)\right]^{T}+\left(\boldsymbol{b}^{(3)}\right)^{T}} $
即:
${\Large z_{6}=w_{(4,6)} * f_{4}\left(z_{4}\right)+w_{(5,6)} * f_{5}\left(z_{5}\right)+b_{6}} $
因为该网络要解决的是一个二分类问题,所以输出层的激活函数也可以使用一个Sigmoid型函数,神经网络最后的输出为:$f_{6}\left(z_{6}\right)$
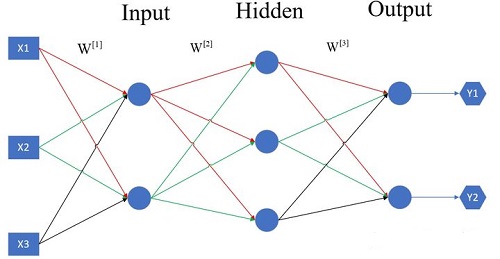
网络结构:
以上图的网络结构为例, 输入数据是 $X=\left[\begin{array}{cc}x_{1}^{(1)} & x_{1}^{(2)} \\ x_{2}^{(1)} & x_{2}^{(2)} \\ x_{3}^{(1)} & x_{3}^{(2)}\end{array}\right]_{3 \times 2} $, 其中包括 2 个样本, 每个样本都有3个特征,即 $X$ 的行数=特征个数, 列数=样本总数。记 $A^{[0]}=X$ , 圆括号表示第几个样 本,方括号表示第几层,下角标是特征的个数。
一、输入层(Input)
权重和偏执项 $W^{[1]}=\left[\begin{array}{ccc}w_{11}^{[1]} & w_{12}^{[1]} & w_{13}^{[1]} \\ w_{21}^{[1]} & w_{22}^{[1]} & w_{23}^{[1]}\end{array}\right]_{2 \times 3}, \quad B^{[1]}=\left[\begin{array}{c}b_{1}^{[1]} \\ b_{2}^{[1]}\end{array}\right]_{2 \times 1} $
W 的行数=当前层神经元的个数, 列数=当前层所接受的特征个数。
B 的行数=当前层神经元的个数。
该层的线性计算:(这里其实用了类似Python中广播的概念,否则的话 $B$ 的列数与前一项不相等,按照基本的矩阵加法,这是没法加的)
$Z^{[1]}=W^{[1]} A^{[0]}+B^{[1]}=\left[\begin{array}{cc} w_{11}^{[1]} x_{1}^{(1)}+w_{12}^{[1]} x_{2}^{(1)}+w_{13}^{[1]} x_{3}^{(1)}+b_{1}^{[1]} & w_{11}^{[1]} x_{1}^{(2)}+w_{12}^{[1]} x_{2}^{(2)}+w_{13}^{[1]} x_{3}^{(2)}+b_{1}^{[1]} \\ w_{21}^{[1]} x_{1}^{(1)}+w_{22}^{[1]} x_{2}^{(1)}+w_{23}^{[1]} x_{3}^{(1)}+b_{2}^{[1]} & w_{21}^{[1]} x_{1}^{(2)}+w_{22}^{[1]} x_{2}^{(2)}+w_{23}^{[1]} x_{3}^{(2)}+b_{2}^{[1]} \end{array}\right]_{2 \times 2}$
记作
$Z^{[1]}=\left[\begin{array}{cc} z_{1}^{[1](1)} & z_{1}^{[1](2)} \\ z_{2}^{[1](1)} & z_{2}^{[1](2)} \end{array}\right]_{2 \times 2}$
激活输出
$A^{[1]}=\sigma\left(Z^{[1]}\right)=\left[\begin{array}{cc} a_{1}^{[1](1)} & a_{1}^{[1](2)} \\ a_{2}^{[1](1)} & a_{2}^{[1](2)} \end{array}\right]_{2 \times 2}=\left[\begin{array}{ll} \sigma\left(z_{1}^{[1](1)}\right) & \sigma\left(z_{1}^{[1](2)}\right) \\ \sigma\left(z_{2}^{[1](1)}\right) & \sigma\left(z_{2}^{[1](2)}\right) \end{array}\right]_{2 \times 2}$
二、隐含层(Hidden)
权重和偏执项
$W^{[2]}=\left[\begin{array}{cc} w_{11}^{[2]} & w_{12}^{[2]} \\ w_{21}^{[2]} & w_{22}^{[2]} \\w_{31}^{[2]} & w_{32}^{[2]} \end{array}\right]_{3 \times 2}, B^{[2]}=\left[\begin{array}{c} b_{1}^{[2]} \\ b_{2}^{[2]} \\ b_{3}^{[2]} \end{array}\right]_{3 \times 1}$
该层的线性计算
$Z^{[2]}=W^{[2]} A^{[1]}+B^{[2]}=\left[\begin{array}{ll} w_{11}^{[2]} a_{1}^{[1](1)}+w_{12}^{[2]} a_{2}^{[1](1)}+b_{1}^{[2]} & w_{11}^{[2]} a_{1}^{[1](2)}+w_{12}^{[2]} a_{2}^{[1](2)}+b_{1}^{[2]} \\ w_{21}^{[2]} a_{1}^{[1](1)}+w_{22}^{[2]} a_{2}^{[1](1)}+b_{2}^{[2]} & w_{21}^{[2]} a_{1}^{[1](2)}+w_{22}^{[2]} a_{2}^{[1](2)}+b_{2}^{[2]} \\ w_{31}^{[2]} a_{1}^{[1](1)}+w_{32}^{[2]} a_{2}^{[1](1)}+b_{3}^{[2]} & w_{31}^{[2]} a_{1}^{[1](2)}+w_{32}^{[2]} a_{2}^{[1](2)}+b_{3}^{[2]} \end{array}\right]_{3 \times 2}$
记作
$Z^{[2]}=\left[\begin{array}{cc} z_{1}^{[2](1)} & z_{1}^{[2](2)} \\ z_{2}^{[2](1)} & z_{2}^{[2](2)} \\ z_{3}^{[2](1)} & z_{3}^{[2](2)} \end{array}\right]_{3 \times 2}$
激活输出
$A^{[2]}=\sigma\left(Z^{[2]}\right)=\left[\begin{array}{cc} a_{1}^{[2](1)} & a_{1}^{[2](2)} \\ a_{2}^{[2](1)} & a_{2}^{[2](2)} \\ a_{3}^{[2](1)} & a_{3}^{[2](2)} \end{array}\right]_{3 \times 2}=\left[\begin{array}{cc} \sigma\left(z_{1}^{[2](1)}\right) & \sigma\left(z_{1}^{[2](2)}\right) \\ \sigma\left(z_{2}^{[2](1)}\right) & \sigma\left(z_{2}^{[2](2)}\right) \\ \sigma\left(z_{3}^{[2](1)}\right) & \sigma\left(z_{3}^{[2](2)}\right) \end{array}\right]_{3 \times 2}$
三、输出层(Output)
权重和偏执项
$W^{[3]}=\left[\begin{array}{ccc} w_{11}^{[3]} & w_{12}^{[3]} & w_{13}^{[3]} \\ w_{21}^{[3]} & w_{22}^{[3]} & w_{23}^{[3]} \end{array}\right]_{2 \times 3}, \quad B^{[3]}=\left[\begin{array}{c} b_{1}^{[3]} \\ b_{2}^{[3]} \end{array}\right]_{2 \times 1}$
该层的线性计算
$Z^{[3]}=W^{[3]} A^{[2]}+B^{[3]}=\left[\begin{array}{ll} w_{11}^{[3]} a_{1}^{[2](1)}+w_{12}^{[3]} a_{2}^{[2](1)}+w_{13}^{[3]} a_{3}^{[2](1)}+b_{1}^{[3]} & w_{11}^{[3]} a_{1}^{[2](2)}+w_{12}^{[3]} a_{2}^{[2](2)}+w_{13}^{[3]} a_{3}^{[2](2)}+b_{1}^{[3]} \\ w_{21}^{[3]} a_{1}^{[2](1)}+w_{22}^{[3]} a_{2}^{[2](1)}+w_{23}^{[3]} a_{3}^{[2](1)}+b_{1}^{[3]} & w_{21}^{[3]} a_{1}^{[2](2)}+w_{22}^{[3]} a_{2}^{[2](2)}+w_{23}^{[3]} a_{3}^{[2](2)}+b_{1}^{[3]} \end{array}\right]_{2 \times 2}$
记作
$Z^{[3]}=\left[\begin{array}{cc} z_{1}^{[3](1)} & z_{1}^{[3](2)} \\ z_{2}^{[3](1)} & z_{2}^{[3](2)} \end{array}\right]_{2 \times 2}$
激活输出
$A^{[3]}=\sigma\left(Z^{[3]}\right)=\left[\begin{array}{cc} a_{1}^{[3](1)} & a_{1}^{[3](2)} \\ a_{2}^{[3](1)} & a_{2}^{[3](2)} \end{array}\right]_{2 \times 2}=\left[\begin{array}{cc} \sigma\left(z_{1}^{[3](1)}\right) & \sigma\left(z_{1}^{[3](2)}\right) \\ \sigma\left(z_{2}^{[3](1)}\right) & \sigma\left(z_{2}^{[3](2)}\right) \end{array}\right]_{2 \times 2}$
输出结果是
$Y=\left[\begin{array}{cc} y_{1}^{(1)} & y_{1}^{(2)} \\ y_{2}^{(1)} & y_{2}^{(2)}\end{array}\right]_{2 \times 2}=A^{[3]}$
对应的真实标签值记是
$\tilde{Y}=\left[\begin{array}{ll} \tilde{y_{1}}^{(1)} & \tilde{y_{1}}^{(2)} \\ \tilde{y_{2}}^{(1)} & \tilde{y_{2}}^{(2)} \end{array}\right]_{2 \times 2}$
设每个神经元的激活函数为最常用的Sigmoid函数:
$\sigma(z)=\frac{1}{1+e^{-z}}$
分类问题中的BP问题:
目标函数:交叉熵函数
$L=-(\tilde{Y} \log (Y)+(1-\tilde{Y}) \log (1-Y))$
$ {\small =\left[\begin{array}{ll} -\left(\tilde{y}_{1}^{(1)} \log \left(y_{1}^{(1)}\right)+\left(1-\tilde{y_{1}}^{(1)}\right) \log \left(1-y_{1}^{(1)}\right)\right. & -\left(\tilde{y}_{1}^{(2)} \log \left(y_{1}^{(2)}\right)+\left(1-\tilde{y}_{1} ^{(2)}\right) \log \left(1-y_{1}^{(2)}\right)\right) \\ -\left(\tilde{y_{2}}(1) \log \left(y_{2}^{(1)}\right)+\left(1-\tilde{y_{2}}^{(1)}\right) \log \left(1-y_{2}^{(1)}\right)\right. & -\left(\tilde{y}_{2}^{(2)} \log \left(y_{2}^{(2)}\right)+\left(1-\tilde{y_{2}}^ {(2)}\right) \log \left(1-y_{2}^{(2)}\right)\right) \end{array}\right]_{2 \times 2}} $
简记为:
$L=\left[\begin{array}{ll} l_{1}^{(1)} & l_{1}^{(2)} \\ l_{2}^{(1)} & l_{2}^{(2)} \end{array}\right]$
则由简单的链导法则可有:
$\frac{d L}{d Z^{[3]}}=\frac{d L}{d A^{[3]}} \frac{d A^{[3]}}{d Z^{[3]}}=\left[\begin{array}{cc} \frac{d l_{1}^{(1)}}{d a_{1}^{[3](1)}} \frac{d a_{1}^{[3](1)}}{d z_{1}^{[3](1)}} & \frac{d l_{1}^{(2)}}{d a_{1}^{[3](2)}} \frac{d a_{1}^{[3](2)}}{d z_{1}^{[3](2)}} \\ \frac{d l_{2}^{(1)}}{d a_{2}^{[3](1)}} \frac{d a_{2}^{[3](1)}}{d z_{2}^{[3](1)}} & \frac{d l_{2}^{(2)}}{d a_{2}^{[3](2)}} \frac{d a_{2}^{[3](2)}}{d z_{2}^{[3](2)}} \end{array}\right]_{2 \times 2}=\left[\begin{array}{cc} d z_{1}^{[3](1)} & d z_{1}^{[3](2)} \\ d z_{2}^{[3](1)} & d z_{2}^{[3](2)} \end{array}\right]_{2 \times 2}$
记 $\frac{d L}{d Z^{[3]}}=d Z^{[3]}, \frac{d L}{d A^{[3]}}=d A^{[3]}, \frac{d A}{d Z^{[3]}}=\sigma^{\prime}\left(Z^{[3]}\right)$,则,显然有:
$d Z^{[3]}=d A^{[3]} * \sigma^{\prime}\left(Z^{[3]}\right)$,
即:
$\left[\begin{array}{ll} d z_{1}^{[3](1)} & d z_{1}^{[3](2)} \\ d z_{2}^{[3](1)} & d z_{2}^{[3](2)} \end{array}\right]_{2 \times 2}=\left[\begin{array}{ll} d a_{1}^{[3](1)} & d a_{1}^{[3](2)} \\ d a_{2}^{[3](1)} & d a_{2}^{[3](2)} \end{array}\right]_{2 \times 2} *\left[\begin{array}{ll} d \sigma\left(z_{1}^{[3](1)}\right) & d \sigma\left(z_{1}^{[3](2)}\right) \\ d \sigma\left(z_{2}^{[3](1)}\right) & d \sigma\left(z_{2}^{[3](2)}\right) \end{array}\right]_{2 \times 2}$
其中的 $\ast $ 表示逐元素相乘。这一块涉及的函数求导就不赘述了,然后就可很容易计算出来下面的结果:
$d Z^{[3]}=A^{[3]}-\tilde{Y}$
$\frac{d L}{d W^{[3]}}=\frac{d L}{d Z^{[3]}} \frac{d Z^{[3]}}{d W^{[3]}}=\left[\begin{array}{lll} \frac{d l_{1}^{(1)}}{d w_{11}^{[3]}}+\frac{d l_{1}^{(2)}}{d w_{11}^{[3]}} & \frac{d l_{1}^{(1)}}{d w_{12}^{[3]}}+\frac{d l_{1}^{(2)}}{d w_{12}^{[3]}} & \frac{d l_{1}^{(1)}}{d w_{13}^{[3]}}+\frac{d l_{1}^ {(2)}}{d w_{13}^{[3]}} \\ \frac{d l_{2}^{(1)}}{d w_{21}^{[3]}}+\frac{d l_{2}^{(2)}}{d w_{21}^{[3]}} & \frac{d l_{2}^{(1)}}{d w_{22}^{[3]}}+\frac{d l_{2}^{(2)}}{d w_{22}^{[3]}} & \frac{d l_{2}^{(1)}}{d w_{23}^{[3]}}+\frac{d l_{2}^ {(2)}}{d w_{23}^{[3]}} \end{array}\right]_{2 \times 3}$
$d W^{[3]}=\left[\begin{array}{ccc} \frac{d l_{1}^{(1)}}{d z_{1}^{[3](1)}} \frac{d z_{1}^{[3](1)}}{d w_{11}^{[3]}}+\frac{d l_{1}^{(2)}}{d z_{1}^{[3](2)}} \frac{d z_{1}^{[3](2)}}{d w_{11}^{[3]}} & \frac{d l_{1}^{(1)}}{d z_{1}^{[3](1)}} \frac{d z_ {1}^{[3](1)}}{d w_{12}^{[3]}}+\frac{d l_{1}^{(2)}}{d z_{1}^{[3](2)}} \frac{d z_{1}^{[3](2)}}{d w_{12}^{[3]}} & \frac{d l_{1}^{(1)}}{d z_{1}^{[3](1)}} \frac{d z_{1}^{[3](1)}}{d w_{13}^{[3]}}+\frac{d l_{1}^ {(2)}}{d z_{1}^{[3](2)}} \frac{d z_{1}^{[3](2)}}{d w_{13}^{[3]}} \\ \frac{d l_{2}^{[3](1)}}{d z_{2}^{[3](1)}}{d w_{21}^{[3]}}+\frac{d l_{2}^{[2)}}{d z_{2}^{[3](2)}} \frac{d z_{2}^{[3](2)}}{d w_{21}^{[3]}} & \frac{d l_{2}^{(1)}}{d z_{2}^{[3](1)}} \frac{d z_{2}^{[3](1)}}{d w_ {22}^{[3]}}+\frac{d l_{2}^{(2)}}{d z_{2}^{[3](2)}} \frac{d z_{2}^{[3](2)}}{d w_{22}^{[3]}} & \frac{d l_{2}^{(1)}}{d z_{2}^{[3](1)}} \frac{d z_{2}^{[3](1)}}{d w_{23}^{[3]}}+\frac{d l_{2}^{(2)}}{d z_{2}^{[3](2)}} \frac{d z_{2}^{[3](2)}}{d w_{23}^{[3]}} \end{array}\right]_{2 \times 3}$
上式计算后,结果为:
$d W^{[3]}=\left[\begin{array}{lll} d z_{1}^{[3](1)} a_{1}^{[2](1)}+d z_{1}^{[3](2)} a_{1}^{[2](2)} & d z_{1}^{[3](1)} a_{2}^{[2](1)}+d z_{1}^{[3](2)} a_{2}^{[2](2)} & d z_{1}^{[3](1)} a_{3}^{[2](1)}+d z_{1}^{[3](2)} a_{3}^{[2](2)} \\ d z_{2}^{[3](1)} a_{1}^{[2](1)}+d z_{2}^{[3](2)} a_{1}^{[2](2)} & d z_{2}^{[3](1)} a_{2}^{[2](1)}+d z_{2}^{[3](2)} a_{2}^{[2](2)} & d z_{2}^{[3](1)} a_{3}^{[2](1)}+d z_{2}^{[3](2)} a_{3}^{[2](2)} \end{array}\right]_{2 \times 3}$
从上面的式子可以看出,每个权重的梯度是每个样本得到的梯度之和,因此,这里都除以样本个数,求出平均梯度。整理一下,我们就得到:
$d W^{[3]}=\frac{1}{2}\left[\begin{array}{cc} d z_{1}^{[3](1)} & d z_{1}^{[3](2)} \\d z_{2}^{[3](1)} & d z_{2}^{[3](2)} \end{array}\right]_{2 \times 2}\left[\begin{array}{ccc} a_{1}^{[2](1)} & a_{2}^{[2](1)} & a_{3}^{[2](1)} \\ a_{1}^{[2](2)} & a_{2}^{[2](2)} & a_{3}^{[2](2)} \end{array}\right]_{2 \times 3}$
即 $d W^{[3]}=\frac{1}{2} d Z^{[3]} A^{[2]^{T}}$
同理可以求出来:
$d B^{[3]}=\frac{1}{2} d Z^{[3]}\left[\begin{array}{l} 1 \\1 \end{array}\right]$
其实这就是$d Z^{[3]}$按行求和(即求第一行的总和,第二行的总和),所以简写为(Python中numpy的sum函数):
$d B^{[3]}=\frac{1}{2} \operatorname{sum}\left(d Z^{[3]}, a x i s=1\right)$
现在输出层的都求出来,然后就再往回一层,求隐含层的梯度,因此,中间链导需要经过$A^{[2]}$:
$d A^{[2]}=\left[\begin{array}{ll} d z_{1}^{[3](1)} \frac{d z_{1}^{[3](1)}}{d a_{1}^{[2](1)}}+d z_{2}^{[3](1)} \frac{d z_{2}^{[3](1)}}{d a_{1}^{[2](1)}} \quad d z_{1}^{[3](2)} \frac{d z_{1}^{[3](2)}}{d a_{1}^{[2](2)}}+d z_{2}^{[3](2)} \frac{d z_{2}^{[3](2)}}{d a_{1}^{[2](2)}} \\ d z_{1}^{[3](1)} \frac{d z_{2}^{[3](1)}}{d a_{2}^{[2](1)}}+d z_{2}^{[3](1)} \frac{d z_{2}^{[3](1)}}{d a_{2}^{[2](1)}} \quad d z_{1}^{[3](2)} \frac{d z_{1}^{[3](2)}}{d a_{2}^{[2](2)}}+d z_{2}^{[3](2)} \frac{d z_{2}^{[3](2)}}{d a_{2}^{[2](2)}} \\ d z_{1}^{[3](1)} \frac{d z_{1}^{[3](1)}}{d a_{3}^{[2](1)}}+d z_{2}^{[3](1)} \frac{d z_{2}^{[3](1)}}{d a_{3}^{[2](1)}} \quad d z_{1}^{[3](2)} \frac{d z_{1}^{[3](2)}}{d a_{3}^{[2](2)}}+d z_{2}^{[3](2)} \frac{d z_{2}^{[3](2)}}{d a_{3}^{[2](2)}} \end{array}\right]_{3 \times 2}$
$d A^{[2]}=\left[\begin{array}{ll} d z_{1}^{[3](1)} w_{11}^{[3]}+d z_{2}^{[3](1)} w_{21}^{[3]} & d z_{1}^{[3](2)} w_{11}^{[3]}+d z_{2}^{[3](2)} w_{21}^{[3]} \\ d z_{2}^{[3](1)} w_{12}^{[3]}+d z_{2}^{[3](1)} w_{22}^{[3]} & d z_{1}^{[3](2)} w_{12}^{[3]}+d z_{2}^{[3](2)} w_{22}^{[3]} \\ d z_{1}^{[3](1)} w_{13}^{[3]}+d z_{2}^{[3](1)} w_{23}^{[3]} & d z_{1}^{[3](2)} w_{13}^{[3]}+d z_{2}^{[3](2)} w_{23}^{[3]} \end{array}\right]_{3 \times 2}$
即:
$d A^{[2]}=W^{[3]^{T}} d Z^{[3]}$
接着就可以计算
$d Z^{[2]}=d A^{[2]} * \sigma^{\prime}\left(Z^{[2]}\right)$
然后就可以推导隐含层的梯度了,过程和上面是一样的,就不再写那么一大堆了,直接给出结果:
$d W^{[2]}=\frac{1}{2} d Z^{[2]} A^{[1]^{T}}$
$d B^{[2]}=\frac{1}{2} \operatorname{sum}\left(d Z^{[2]}, \text { axis }=1\right)$
同理,计算$d A^{[1]}, \quad d Z^{[1]}$ ,于是就可得输入层的梯度:
$d W^{[1]}=\frac{1}{2} d Z^{[1]} A^{[0]^{T}}$
$d B^{[1]}=\frac{1}{2} \operatorname{sum}\left(d Z^{[1]}, a x i s=1\right)$
然后更新权重即可:
$\begin{array}{c} W^{[i]}=W^{[i]}-\eta d W^{[i]} \\ B^{[i]}=B^{[i]}-\eta d B^{[i]} \\ i=1,2,3 \end{array}$
参考博客《神经网络BP算法推导》
假设,有这样一个网络层:
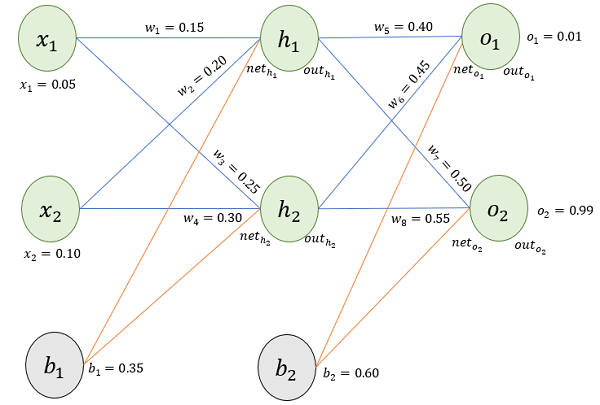
第一层是输入层,包含两个神经元 $x_1$,$x_2$,和截距项 $b_1$;
第二层是隐含层,包含两个神经元 $h_1$,$h_2$ 和截距项 $b_2$,
第三层是输出$o_1$,$o_2$,每条线上标的 $w_i$ 是层与层之间连接的权重,激活函数默认为 Sigmoid函数。
输入数据 $x_1=0.05,x_2=0.10$;
输出数据 $o_1=0.01,o_2=0.99$
初始权重 $w_1=0.15,w_2=0.20,w_3=0.25,w_4=0.30,w_5=0.40,w_6=0.45,w_7=0.50,w_8=0.55$
目标:给出输入数据$x_1 =0.05 ,\ x_2=0.10 $ ,使输出尽可能与原始输出 $o_1=0.01,o_2=0.99$ 接近。
1)输入层——>隐含层:
计算神经元 $h_1$ 的输入加权和:
${\large \begin{array}{l} net_{h 1}=w_{1} * x_{1}+w_{2} * x_{2}+b_{1} \\ n e t_{h 1}=0.15 * 0.05+0.2 * 0.1+0.35=0.3775 \end{array}} $
神经元 $h_1$ 的输出 $o_1$:
$ {\large out _{h1}=\frac{1}{ 1+e^{-net_{h1}} }=\frac{1}{1+e^{-0.3775}}=0.593269992} $
同理,可计算出神经元 $h2$ 的输出 $o2$ :
${\large \begin{array}{l} net_{h2}=w_{3} * x_{1}+w_{4} * x_{2}+b_{1} \\ net_{h2}=0.25 * 0.05+0.30 * 0.10+0.35=0.3925 \end{array}} $
${\large \text { out }_{h 2}=0.596884378} $
2)隐含层——>输出层:
计算输出层神经元 $o_1$ 和 $o_2$ 的值:
${\large \begin{array}{l} \text { net }_{o_1}=w_{5} * \text { out }_{h_1}+w_{6} * \text { out }_{h_2}+b_{2} * 1 \\ \text { net }_{o_1}=0.4 * 0.593269992+0.45 * 0.596884378+0.6 * 1=1.105905967 \\ \text { out }_{o_1}=\frac{1}{1+e^{- net _{o_1}}}=\frac{1}{1+e^{-1.105905967}}=0.75136507 \end{array}} $
${\large \begin{array}{l} \text { net }_{o_2}=w_{7} * \text { out }_{h_1}+w_{6} * \text { out }_{h_2}+b_{2} * 1 \\ \text { net }_{o_2}=0.5 * 0.593269992+0.55 * 0.596884378+0.6 =1.0607782 \\ \text { out }_{o_2}=\frac{1}{1+e^{- net _{o_2}}}=\frac{1}{1+e^{-1.0607782}}=0.772928465 \end{array}} $
前向传播的过程结束得到输出值为 $[0.75136079 , 0.772928465]$,与实际值 $[0.01 , 0.99]$ 相差还很远,现在我们对误差进行反向传播,更新权值,重新计算输出。
1)计算总误差
总误差:
${\large E_{\text {total }}=\sum \frac{1}{2}(\text { target }-\text { output })^{2}} $
但是有两个输出,所以分别计算 $o_1$ 和 $o_2$ 的误差,总误差为两者之和:
${\large E_{o_1}=\frac{1}{2}\left(\text { target }_{o 1}-\text { out }_{o 1}\right)^{2}=\frac{1}{2}(0.01-0.75136507)^{2}=0.274811083} $
${\large E_{o_2}=\frac{1}{2}\left(\text { target }_{o_2}-\text { out }_{o_2}\right)^{2}=\frac{1}{2}(0.99-0.772928465)^{2}=0.023560026} $
${\large E_{\text {total }}=E_{o_1}+E_{o_2}=0.274811083+0.023560026=0.298371109 } $
2)隐含层——>输出层的权值更新:
以权重参数 $w_5$ 为例,我们想知道 $w_5$ 对整体误差产生了多少影响,可以用整体误差对 $w_5$ 求偏导求出:
${\large \frac{\partial E_{\text {total }}}{\partial w_{5}}=\frac{\partial E_{\text {total }}}{\partial \text { out }_{o 1}} * \frac{\partial \text { out }_{o 1}}{\partial \text { net }_{o 1}} * \frac{\partial \text { net }_{o 1}}{\partial w_{5}}} $
下面的图可以更直观的看清楚误差是怎样反向传播的:
${\large \frac{\partial n e t_{o_1}}{\partial w_{5}} * \frac{\partial out_{o_1}}{\partial n e t_{o_1}} * \frac{\partial E_{\text {total }}}{\partial o u t_{o_1}}=\frac{\partial E_{\text {total }}}{\partial w_{5}}} $
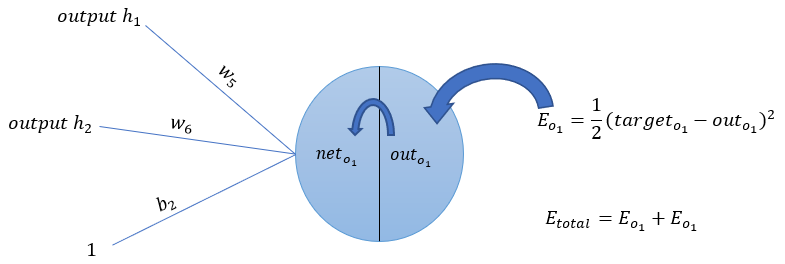
现在分别计算每个式子的值:
1)计算 ${\large \frac{\partial E_{\text {total }}}{\partial o u t_{o 1}}} $ :
${\large \begin{array}{l} E_{\text {total }}=\frac{1}{2}\left(\text { target }_{o_1}-\text { out }_{o_1}\right)^{2}+\frac{1}{2}\left(\text { target }_{o_2}-o u t_{o_2}\right)^{2} \\ \frac{\partial E_{\text {total }}}{\partial \text { out}_{o_1}}=2 * \frac{1}{2}\left(\text { target }_{o_1}-\text { out }_{o_1}\right)^{2-1} *-1+0 \\ \frac{\partial E_{\text {total }}}{\partial \text { out }_{o_1}}=-\left(\text { target }_{o_1}-\text { out }_{o_1}\right)=-(0.01-0.75136507)=0.74136507 \end{array}} $
2)计算 ${\large \frac{\partial out_{o_1}}{\partial net_{o_1}}} $
${\large\begin{array}{l} \text { out }_{o_1}=\frac{1}{1+e^{-n e t_{o_1}}} \\ \frac{\partial \text { out }_{o_1}}{\partial\ \text { net} _{o_1}}=\text { out }_{o_1}\left(1-\text { out }_{o_1}\right)=0.75136507(1-0.75136507)=0.186815602 \end{array}}$
3)计算 ${\large \frac{\partial n e t_{o_1}}{\partial w_{5}}} $
${\large \begin{array}{l} \text { net }_{o_1}=w_{5} * \text { out }_{h_1}+w_{6} * \text { out }_{h_2}+b_{2} * 1 \\ \frac{\partial n e t_{o_1}}{\partial w_{5}}=1 * \text { out }_{h_1}+0+0=\text { out }_{h_1}=0.593269992 \end{array}} $
最后三者相乘:
$ {\large \begin{aligned} \frac{\partial E_{\text {total }}}{\partial w_{5}} &=\frac{\partial E_{\text {total }}}{\partial \text { out }_{o_1}} * \frac{\partial \text { out }_{o_1}}{\partial \text { net }_{o_1}} * \frac{\partial \text { net }_{o_1}}{\partial w_{5}} \\ \frac{\partial E_{\text {total }}}{\partial w_{5}} &=0.74136507 * 0.186815602 * 0.593269992=0.082167041 \end{aligned} } $
这样就计算出整体误差 $E(total)$ 对 $w_5$ 的偏导值。
回过头来看上面的公式,发现:
${\large \frac{\partial E_{\text {total }}}{\partial w_{5}}=-\left(\operatorname{target}_{o_1}-\text { out }_{o_1}\right) * \text { out }_{o_1}\left(1-\text { out }_{o_1}\right) * \text { out }_{h_1}} $
为表达方便,用 $\delta_{o 1}$ 来表示输出层的误差:
$ {\large \begin{array}{l} \delta_{o_1}=\frac{\partial E_{\text {total }}}{\partial o u t_{o_1}} * \frac{\partial o u t_{o_1}}{\partial n e t_{o_1}}=\frac{\partial E_{\text {total }}}{\partial n e t_{o_1}} \\ \delta_{o_1}=-\left(\text { target }_{o_1}-\text { out }_{o_1}\right) * \text { out }_{o_1}\left(1-\text { out }_{o_1}\right) \end{array} } $
因此,整体误差 $E(total)$ 对 $w_5$ 的偏导公式可以写成:
$\frac{\partial E_{\text {total }}}{\partial w_{5}}=\delta_{o 1} \text { out }_{h 1}$
如果输出层误差计为负的话,也可以写成:
$\frac{\partial E_{\text {total }}}{\partial w_{5}}=-\delta_{o_1} \text { out }_{h_1}$
最后更新 $w_5$ 的值:(其中,$\eta$ 是学习速率,这里取 $0.5$ )
$w_{5}^{+}=w_{5}-\eta * \frac{\partial E_{\text {total }}}{\partial w_{5}}=0.4-0.5 * 0.082167041=0.35891648$
同理,可更新 $w_6\ ,w_7 \ ,w_8$:
$ \begin{aligned} w_{6}^{+} &=0.408666186 \\ w_{7}^{+} &=0.511301270 \\ w_{8}^{+} &=0.561370121 \end{aligned} $
3)隐含层——>输入层的权值更新:
方法其实与上面说的差不多,但是有个地方需要变一下,在上文计算总误差对 $w_5$ 的偏导时,是从 $out_{o_1}$->$net_{o_1}$->$w_5$ ,但是在隐含层之间的权值更新时,是 $out_{h1}$->$net_{h1}$->$w_1$,而 $out_{h_1}$ 会接受 $E_{o_1}$ 和 $E_{o_2}$ 两个地方传来的误差,所以这个地方两个都要计算。
$\frac{\partial E_{\text {total }}}{\partial w_{1}}= \frac{\partial E_{\text {total }}}{\partial \text { out }_{h_1}} * \frac{\partial \text { out }_{h_1}}{\partial n e t_{h_1}} * \frac{\partial \text { net }_{h_1}}{\partial w_{1}} $
$\frac{\partial E_{\text {total }}}{\partial o u t_{h_1}}=\frac{\partial E_{o_1}}{\partial o u t_{h_1}}+\frac{\partial E_{o_2}}{\partial \text { out }_{h_1}}$
计算 $\frac{\partial E_{\text {total }}}{\partial o u t_{h_1}}$
${\large \frac{\partial E_{\text {total }}}{\partial \text { out }_{h_1}}=\frac{\partial E_{o_1}}{\partial o u t_{h_1}}+\frac{\partial E_{o_2}}{\partial o u t_{h_1}}}$
先计算 $\frac{\partial E_{o_1}}{\partial o u t_{h_1}}$
${\large \frac{\partial E_{o_1}}{\partial o u t_{h_1}}=\frac{\partial E_{o_1}}{\partial n e t_{o_1}} * \frac{\partial n e t_{o_1}}{\partial o u t_{h_1}}} $
${\large \frac{\partial E_{o_1}}{\partial n e t_{o_1}}=\frac{\partial E_{o_1}}{\partial o u t_{o_1}} * \frac{\partial o u t_{o_1}}{\partial n e t_{o_1}}=0.74136507 * 0.186815602=0.138498562} $
${\large n e t_{o_1}=w_{5} * \text { out }_{h 1}+w_{6} * \text { out }_{h_2}+b_{2} * 1} $
${\large \frac{\partial \text { net }_{o_1}}{\partial \text { out }_{h_1}}=w_{5}=0.40} $
${\large \frac{\partial E_{o_1}}{\partial o u t_{h_1}}=\frac{\partial E_{o_1}}{\partial n e t_{o_1}} * \frac{\partial n e t_{o_1}}{\partial o u t_{h_1}}=0.138498562 * 0.40=0.055399425} $
同理,计算出:
${\large \frac{\partial E_{o_2}}{\partial o u t_{h_1}}=-0.019049119} $
两者相加得到总值:
${\large \frac{\partial E_{\text {total }}}{\partial o u t_{h_1}}=\frac{\partial E_{o_1}}{\partial o u t_{h_1}}+\frac{\partial E_{o_2}}{\partial o u t_{h_1}}=0.055399425+-0.019049119=0.036350306} $
再计算 ${\large \frac{\partial o u t_{h_1}}{\partial n e t_{h_1}}} $
${\large \text { out }_{h_1}=\frac{1}{1+e^{-net_{h_1}} }} $
${\large \frac{\partial o u t_{h_1}}{\partial n e t_{h_1}}=o u t_{h_1}\left(1-o u t_{h_1}\right)=0.59326999(1-0.59326999)=0.241300709} $
再计算 ${\large \frac{\partial \text { net }_{h_1}}{\partial w_{1}}} $
${\large \text { net }_{h 1}=w_{1} * x_{1}+w_{2} * i_{2}+b_{1} * 1} $
${\large \frac{\partial n e t_{h_1}}{\partial w_{1}}=x_{1}=0.05} $
最后,三者相乘:
${\large \frac{\partial E_{\text {total }}}{\partial w_{1}}=\frac{\partial E_{\text {total }}}{\partial o u t_{h_1}} * \frac{\partial o u t_{h_1}}{\partial n e t_{h_1}} * \frac{\partial n e t_{h_1}}{\partial w_{1}}} $
${\large \frac{\partial E_{\text {total }}}{\partial w_{1}}=0.036350306 * 0.241300709 * 0.05=0.000438568} $
为了简化公式,用 $Sigma(h_1)$ 表示隐含层单元 $h_1$ 的误差:
${\large \frac{\partial E_{\text {total }}}{\partial w_{1}}=\left(\sum\limits _{o} \frac{\partial E_{\text {total }}}{\partial o u t_{o}} * \frac{\partial out_o }{\partial net_o} * \frac{\partial net_o }{\partial \text { out }_{h_1}}\right) * \frac{\partial o u t_{h_1}}{\partial n e t_{h_1}} * \frac{\partial \text { net }_{h 1}}{\partial w_{1}}} $
${\large \frac{\partial E_{\text {total }}}{\partial w_{1}}=\left(\sum \limits _{o} \delta_{o} * w_{h_o}\right) * out _{h_1}\left(1-\text { out }_{h 1}\right) * x_{1}} $
${\large \frac{\partial E_{\text {total }}}{\partial w_{1}}=\delta_{h_1} x_{1}} $
最后,更新 $w_1$ 的权值:
${\large w_{1}^{+}=w_{1}-\eta * \frac{\partial E_{\text {total }}}{\partial w_{1}}=0.15-0.5 * 0.000438568=0.149780716} $
同理,可更新 $w_2,w_3,w_4$ 的权值:
${\large \begin{array}{l} w_{2}^{+}=0.19956143 \\ w_{3}^{+}=0.24975114 \\ w_{4}^{+}=0.29950229 \end{array}} $
这样误差反向传播法就完成了,最后我们再把更新的权值重新计算,不停地迭代,在这个例子中第一次迭代之后,总误差 $E_{total} $ 由 $ 0.298371109 $下降至 $0.291027924$ 。迭代 $10000 $次后,总误差为 $0.000035085$,输出为$[0.015912196,0.984065734]$(原输入为 $[0.01,0.99]$ ),证明效果还是不错的。
文献:
1:一文彻底搞懂BP算法:原理推导+数据演示+项目实战(上篇)
视频:
原文:https://www.cnblogs.com/BlairGrowing/p/14982115.html