函数说明:UG中向量与矩阵相乘使用UF_MTX3_vec_multiply()或者UF_MTX3_vec_multiply_t()函数 ;
UF_MTX3_vec_multiply()函数表示向量(vec) X 矩阵(mtx)。
UF_MTX3_vec_multiply_t()函数表示向量(vec) X 矩阵的转置(trns(mtx))。
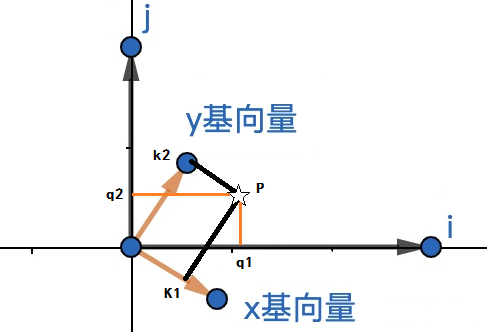
一. 向量 X 矩阵的转置 (vec X trns(mtx))。
设p点在x-y坐标系下坐标是 ;在i-j坐标系下是
,未知的。
x基向量在i-j的坐标是 ,
,
y基向量在i-j的坐标是 ,
,则
那么, ,
,
注意: 是正交矩阵是坐标系矩阵i-j的转置矩阵。
所以想要求的坐标系i-j下的点P(q1,q2)的坐标
只需要把点P(k1,k2)的坐标乘以坐标系矩阵i-j的转置矩阵就可以。
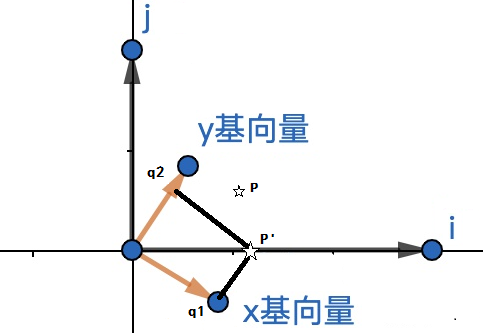
二. 向量 X 矩阵 (vec X mtx)。
向量 X 矩阵就相当于 => 向量 X (矩阵的转置矩阵)的转置
还按上一题的条件,若点P(k1,k2)的坐标乘以坐标系坐标系矩阵i-j。
所以求得就是的 坐标系i-j矩阵的转置矩阵 下的点P’(q1,q2)的坐标。
坐标系i-j矩阵是正交矩阵,它的转置矩阵就是它的逆矩阵。
也就是说:若坐标系i-j矩阵是由基础坐标系x-y逆时针旋转θ°得到,那么坐标系i-j矩阵的逆矩阵就是由基础坐标系x-y逆时针旋转-θ°得到
P’的位置像相当于向量OP点绕原点逆时针旋转-θ°后P的位置。
原文:https://www.cnblogs.com/zmy--blog/p/14972630.html