3.1.2 两条直线平等与垂直的判定

设两条直线 \(l_1，l_2\) 的斜率分别为 \(k_1，k_2\).
若 \(l_1 // l_2\)，则 \(l_1\) 与 \(l_2\) 的倾斜角 \(a_1\) 与 \(a_2\) 相等，如下图，由 \(a_1=a_2\)，可得 \(tan \ a_1=tan \ a_2\)，即 \(k_1=k_2\)，因此
若 \(l_1 // l_2\)，则 \(k_1=k_2\).

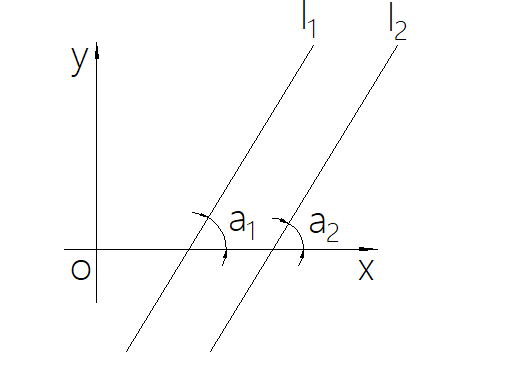
如下图：如果 \(l_1\) 垂直于 \(l_2\) 那么

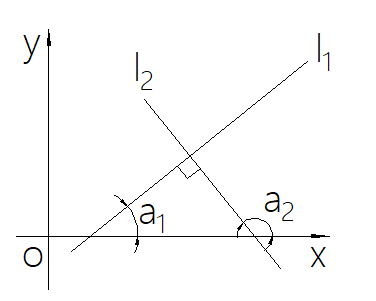
\(tan \ a_2=tan(90^o+a_1)=- \frac{1}{tan \ a_1}\)
即，斜率
\(k_1 k_2=-1\)

3.1.2 两条直线平等与垂直的判定

原文：https://www.cnblogs.com/kingBook/p/14994511.html