408算法练习——盛水最多的容器

盛水最多的容器

原题链接：https://leetcode-cn.com/problems/container-with-most-water/

一、问题描述

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

 示例1：

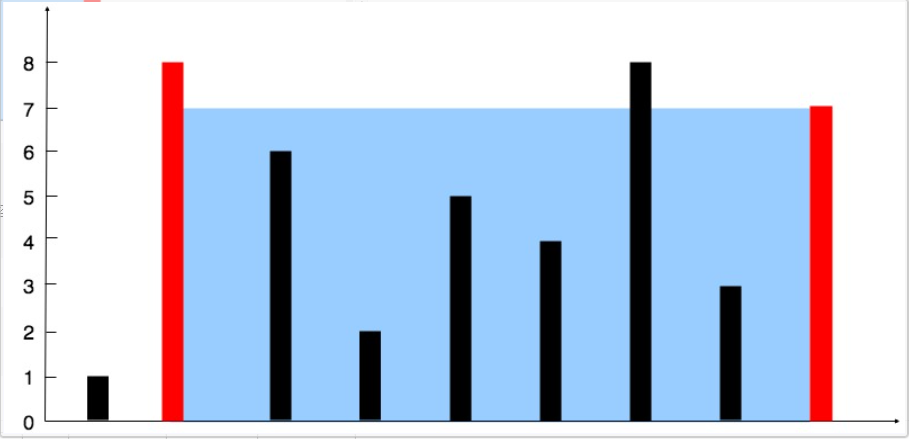
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

示例 3：

输入：height = [4,3,2,1,4]
输出：16

示例 4：

输入：height = [1,2,1]
输出：2

二、问题分析

　　这道题左呈云的课里说过，其实把问题简化就是找出整个数组中两个最大值，记录下面然后计算一个乘积就行，因为木桶原理，所以能装多少水应该以最短的算起。

　　解题：优先现在考虑一个问题，如果在两侧的桶壁比较低，而靠近中点的桶壁又很高，这样就会带来一个问题，就是如果取靠外的边作为桶壁，那么这个桶很宽而矮，而取靠近内测的边作桶壁，这个桶就高而细。而为了求得最大容量每次移动指针的时候都应该计算一次容量。

三、算法实现

　　首先需要的变量：i,j分别指向数组两侧；maxcap，记录最大容量；

　　1、让i和j分别指向数组两端，令maxcap=max（maxcap，j-i(min(i.value,j.value))）//容量等于i和j的距离乘i和j中最小值

　　2、让i.value和j.value中最小值向中间移动，if(i.value<j.value) i++;if(j.value<=i.value) j--; 等号位置随意

　　3、当i=j时结束循环。

 1 class Solution {
 2     public int maxArea(int[] height) {
 3         int i=0,j=height.length-1,maxcap=0;
 4         while(i < j){
 5             maxcap = Math.max(maxcap,(j-i)*(Math.min(height[i],height[j])));
 6             if(height[i]<height[j]){
 7                 i++;
 8             }else{
 9                 j--;
10             }
11         }
12         return maxcap;
13     }
14 }

四、附加问题

　　如果把这个题改一改，不要求最大边作容量，而是要求以左右两个端点作边，这个容器最多能装多少水，那么这道题应该怎么解呢？

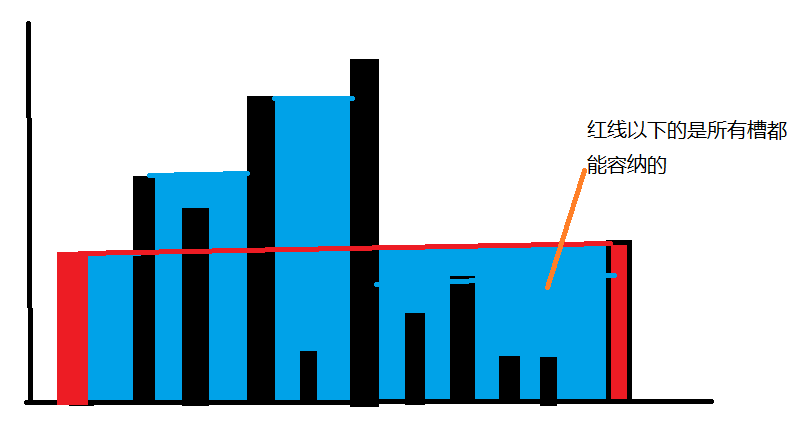
 　　解题思路：就像俄罗斯方块一样，可以一层一层的相消，然后累加起来，在初始时固定最外侧两边，然后计算以这两条边为界能容纳的水量，那么这个水量是所有槽都能容纳下的。然后向内测找边，找一个两端都高于初始边的槽，减去量端边的小值，计算水量，然后累加，依次类推

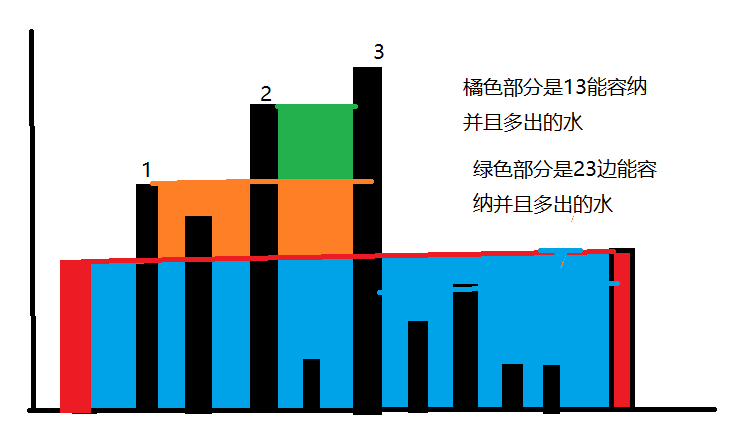
 　　就像图示一样，这样一层一层的计算水量也许是一种可行的办法。

408算法练习——盛水最多的容器

原文：https://www.cnblogs.com/zyq79434/p/15003942.html