------------恢复内容开始------------
###基本概念和术语###
数据:可输入计算机,能够被处理的各种符号集合。
数据元素:数据的基本单位 。
数据项:组成数据元素的不可分割最小单位。
数据对象:性质同的元素集合,是数据子集。
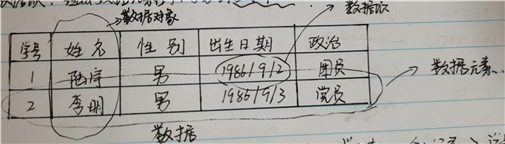
以学生信息表为例。解释:整个表可以看作是一个数据;每一个人所在行就是一个人的全部信息,构成一个个人单位,是一个数据元素;姓名这一列,出生日期这一列,具有相同性质(都是一个人的称号,都是一个人的生日),这就是数据对象;而具体到每一个格子里的内容,就是数据项,这是表格的最小单位(不可再分)。
==============================================================================================================================================================
###数据结构###
数据元素不是孤立存在的,它们存在某种关系,称为结构。其实数据结构就是数据及它们的关系。
主要包括以下三个方面:
1.数据元素之间的逻辑关系,称逻辑结构。
2.数据元素及内在关系在计算机内存中的表示(映像),称物理结构或储存结构。
3.数据运算实现,及对数据元素的操作。
==============================================================================================================================================================
###抽象数据类型###
(Abstract Data Type, ADT) 是指一个数学模型,以及对它操作。
对它的定义需要满足(D,S,P)三元组。
D:数据对象; S:数据对象满足的关系; P:对数据对象的操作;
定义满足以下格式:
ADT 抽象数据类型名称 {
数据对象: <D定义>;
数据关系: <S定义>;
基本操作: <基本操作的定义>;
} ADT 抽象数据类型名称
例如:现在我要定义一个?,以及对圆圈的操作。
ADT CITCLE {
数据对象:D = {r, x, y| r, x, y ∈ R};
数据关系:R = {<r, x, y>| r为半径,(x, y)为圆心坐标};
基本操作:
circle(&C, r, x, y); //构造? 其中&是引用型参数符号,表示C除了提供参数以外,同时接收返回值。就是自己参与,自己接受返回值。
double area(C); //求面积
double circumference(C) //求周长
} ADT CIRCLE;
PS:这里是一种定义的基本方式,只是为你提供了定义一个抽象类型的格式,并不是具体到某一种语言中定义。作为思想。
==============================================================================================================================================================
###算法介绍(了解)###
定义:指定的有限序列。
特性:有穷性(步骤上,时间上);确定性;可行性;输入(零个或者多个输入);输出(至少一个,否则算法无任何意义)。
要求:正确性;可读性;健壮性(鲁棒性):对于非法输入有能力处理;高效性。
==============================================================================================================================================================
###时间效率和空间效率###
算法效率分为:时间效率和空间效率。
算法消耗的时间 = ∑ (单个简单操作时间 × 次数)//这边的次数我们把它叫做”频度“。而简单操作时间取决于硬件软件,这是与算法本身无关的,所以研究问题,我们取它为1。
那么上面式子就是:time = ∑ 次数
例子:计算下列程式消耗时间。
for (i = 1; i <= n; i++) //n+1次(最后一次跳出循环外加一次)
for (j = 1; j <= n; j++) { //n(n+1)次, 这一条是上一条语句循环n次的循环体,本身走n+1次,故循环n(n+1)次
c[i][j] = 0; //n*n次
for (k = 0; k < n; k++) //n*n*(n+1)次
c[i][j] = c[i][j] + a[i][j] * b[i][j]; //n*n*n次
}
把每一个语句执行度相加:T(n) = 2n3 + 3n2 + 2n + 1
为了简化,仅比较数量级(Order)
如果 limn->∞(T(n) / O(f(n)))= C != 0 称 O(f(n))为算法的渐进时间复杂度,简称时间复杂度。
※计算方法:找到算法执行最多的语句,时间复杂度取决于它。找循环嵌套最深的语句。抓大头。
※加法和乘法守则:
1.T(n) = T1(n) + T2(n) = O(f(n)) + O(g(n)) = O(max(f, g))
2.T(n) = T1(n) × T2(n) = O(f(n)) × O(g(n)) = O(f(n) × g(n))
例1:计算下程序时间复杂度。
for (i = 1; i <= n; i++)
for (j = 1; j <= i; j++)
for (k = 1; k <= j; k++)
x += 1;//嵌套最深,单这个语句执行1次。
可以利用级数求和法:
∑(i = 1~n)∑(j = 1~i)∑(k = 1~j)(1) = ∑(i = 1~n)∑(j = 1~i)(j) = ∑(i = 1~n)(i(i+1)/2) = 0.5*(n(n+1)(2n+1)/6 + n(n+1)/2)
T(n) = O(n3)
例2:求下列程序时间复杂度。
i = 1; 1次 => i = 2 要满足循环条件i <= n
while (i <= n) 2次 => i = 4 i = 2f(n) <= n
i *= 2; ................................ f(n) <= log2n
f(n)次 => i = 2f(n) 故 T(n) = O(log2n) 或 O(lgn) //不必可以纠结底是多少,只考虑数量级。
例3:顺序查找, 在数组中查找e元素,返回位置。
for (i = 0; i < n; i++)
if (a[i] == e) return i+1;
return 0;
最好1次找到,最差n次找到,平均n/2次;平均时间复杂度O(n)
PS 时间复杂度:
==============================================================================================================================================================
###时间复杂度比较###
O(1) < O(lgn) < O(n) < O(nlgn) < O(n2) < O(n3) < ... < O(nk) < O(2n)
==============================================================================================================================================================
###渐进空间复杂度###
S(n) = O(f(n)) 算法本身占空间,输入输出,指令,常数,变量等算法要使用得辅助空间。(辅助变量)
例:将一维数组a中n个数逆序放在原数组中
算法1:
for (i = 0; i < n/2; i++) {
t = a[i]; //t就是辅助变量,它得空间是辅助空间。
a[i] = a[n-i-1];
a[n-i-1] = t;
}
//S1(n) = O(1)
算法2:
for (i = 0; i < n; i++)
b[i] = a[n-i-1];
for (i = 0; i < n; i++)
a[i] = b[i];
//S2(n) = O(n)
明显前者空间效率高。
==============================================================================================================================================================
@puitar
以上是绪论中必要知识,最重要是掌握如何分析时间复杂度。
------------恢复内容结束------------
原文:https://www.cnblogs.com/puitar/p/15032893.html