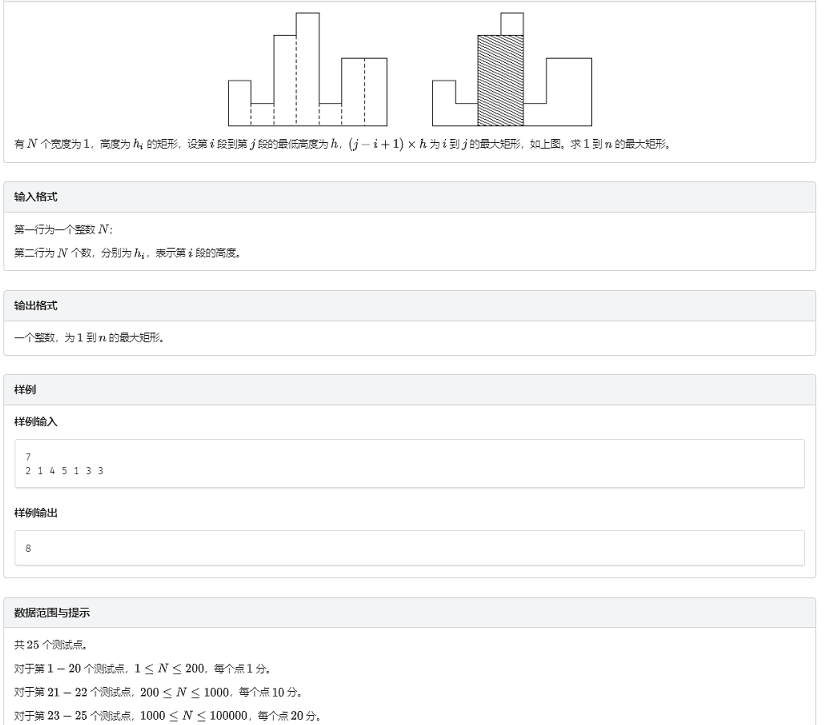
由于放在单调队列章节里当然要考虑用单调队列做
先说下最简单的思路:可以看作动态维护区间最小值,就是和单调队列模板---滑动窗口模型一样,维护一个单调上升的序列,再枚举区间长度,复杂度O(n2),期望得分40分
再说进一步的思路:上一个思路为什么复杂度高,本质在于其枚举区间长度显然是麻烦了。既然对于一个区间,只关心它的区间最小值,那么在找到你一个区间最小值时,肯定是要它的长度越大越好,故不需要枚举区间长度
上述想法反过来进行:对于每个点 i ,用 lst[i] 和 nxt[i] 分别记录从 i 向左或向右走到的最远的点(的下一个点),使满足h[t]>=h[i]这样就只需要O(N)级别的复杂度了
其实只是运用了单调队列的一个思路
代码还有一些细节,注释写了
图示如下
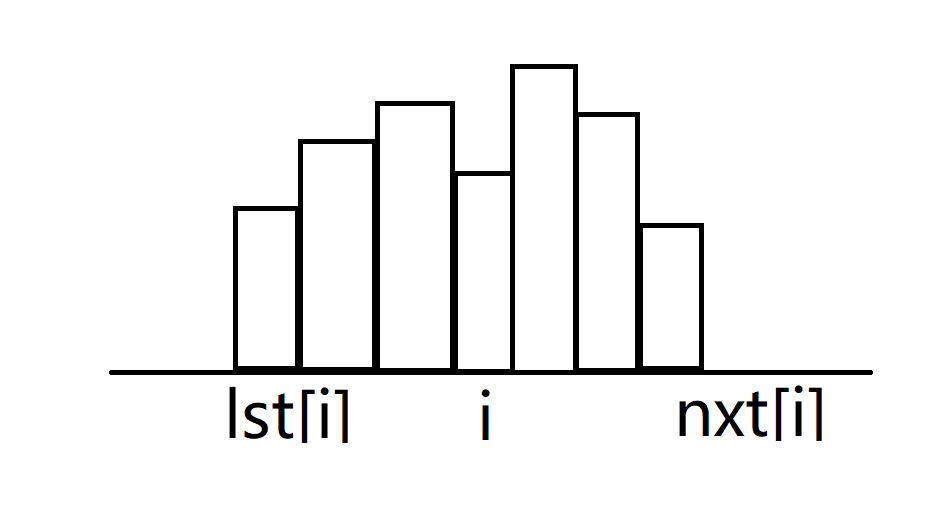
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 1e5+10;
int a[N],n,k;
int p[N],q[N],l=1,r;
int cnt;
int lst[N],nxt[N];//分别表示i向左,向右找到的不小于i的最远点
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
/* 中间while更新不应该用t++、t--会超时
lst[1]=1;
for(int i=2;i<=n;i++)
{
int t=i-1;
while(a[i]<=a[t]&&t>0) t--;
t++;
lst[i]=t;
}
nxt[n]=n;
for(int i=1;i<=n-1;i++)
{
int t=i+1;//写的时候要仔细想好边界条件能否都走到
while(a[i]<=a[t]&&t<=n) t++;
t--;
nxt[i]=t;
}
*/
//lst,nxt的定义都往外移动了1位
lst[1]=0;
for(int i=2;i<=n;i++)
{
int t=i-1;
while(a[i]<=a[t]&&t>0) t=lst[t];
lst[i]=t;
}
nxt[n]=n+1;
for(int i=n-1;i>=1;i--)
{
int t=i+1;
while(a[i]<=a[t]&&t<=n) t=nxt[t];
nxt[i]=t;
}
ll ans=0;
for(int i=1;i<=n;i++)
ans=max(ans,1LL*(nxt[i]-lst[i]-1)*a[i]);
printf("%lld",ans);
return 0;
}
原文:https://www.cnblogs.com/conprour/p/15054220.html