
题目大意:给定一个长度为n的序列,每次操作可以交换任意两个数的位置,代价为两个数的和,求最小代价,将序列排成有序的。
首先,显然需要交换的数一定会形成环:
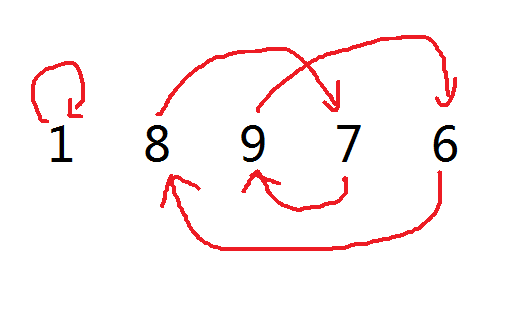
那么对于每一个环,我们有两种选择: 方案1.自己解决自己 ; 方案2.找人来帮助解决。
方案1:用环中的最小值去和其他数交换,代价为 环中数字总和+环中最小值 *(环中数字个数 - 2);
方案2:用整个数列中的最小值去和环中数交换,代价为 环中数字总和+环中最小值 +数列最小值(环中数字个数 + 1)。

#pragma GCC optimize(2) #pragma GCC optimize(3) #include<bits/stdc++.h> using namespace std; int n,S,B[1005],P[1005],Fa[1005],Size[1005],Ans; struct node {int Num,Id;}A[1005]; bool cmp(node x,node y) {return x.Num<y.Num;} #define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++) char buf[65536],*p1,*p2; inline int read() { char ch;int x(0); while((ch=gc)<48); do x=x*10+ch-48;while((ch=gc)>=48); return x; } inline int GetF(int x) { if(x==Fa[x]) return x; return Fa[x]=GetF(Fa[x]); } int main() { for(register int _=1;;++_) { n=read(),Ans=0;if(!n) break; for(register int i=1;i<=n;++i) B[i]=A[i].Num=read(),A[i].Id=i,Fa[i]=i,Size[i]=1; sort(A+1,A+n+1,cmp),S=A[1].Num; for(register int i=1,fx,fy;i<=n;++i) { fx=GetF(i),fy=GetF(A[i].Id),P[A[i].Id]=i; if(fx!=fy) Fa[fy]=fx,Size[fx]+=Size[fy]; } for(register int i=1,x,y,fa,ans,Min;i<=n;++i) { fa=GetF(i); if(!Size[fa]) continue; ans=0,Min=1005,x=i,y=Size[fa]; while(Size[fa]) Min=min(Min,B[x]),ans+=B[x],x=P[x],--Size[fa]; Ans+=min(ans+Min+S*(y+1),ans+Min*(y-2)); } printf("Case %d: %d\n\n",_,Ans); } return 0; }
原文:https://www.cnblogs.com/qfxlzhe/p/15054541.html