426. 将二叉搜索树转化为排序的双向链表

标准的中序遍历采用 左 -> 根 -> 右 的顺序，其中 左 和 右 的部分调用递归。

本题的处理在于将前一个结点与当前结点链接，因此，必须跟踪最后一个结点，该结点在新的双向链表中是当前最大的。

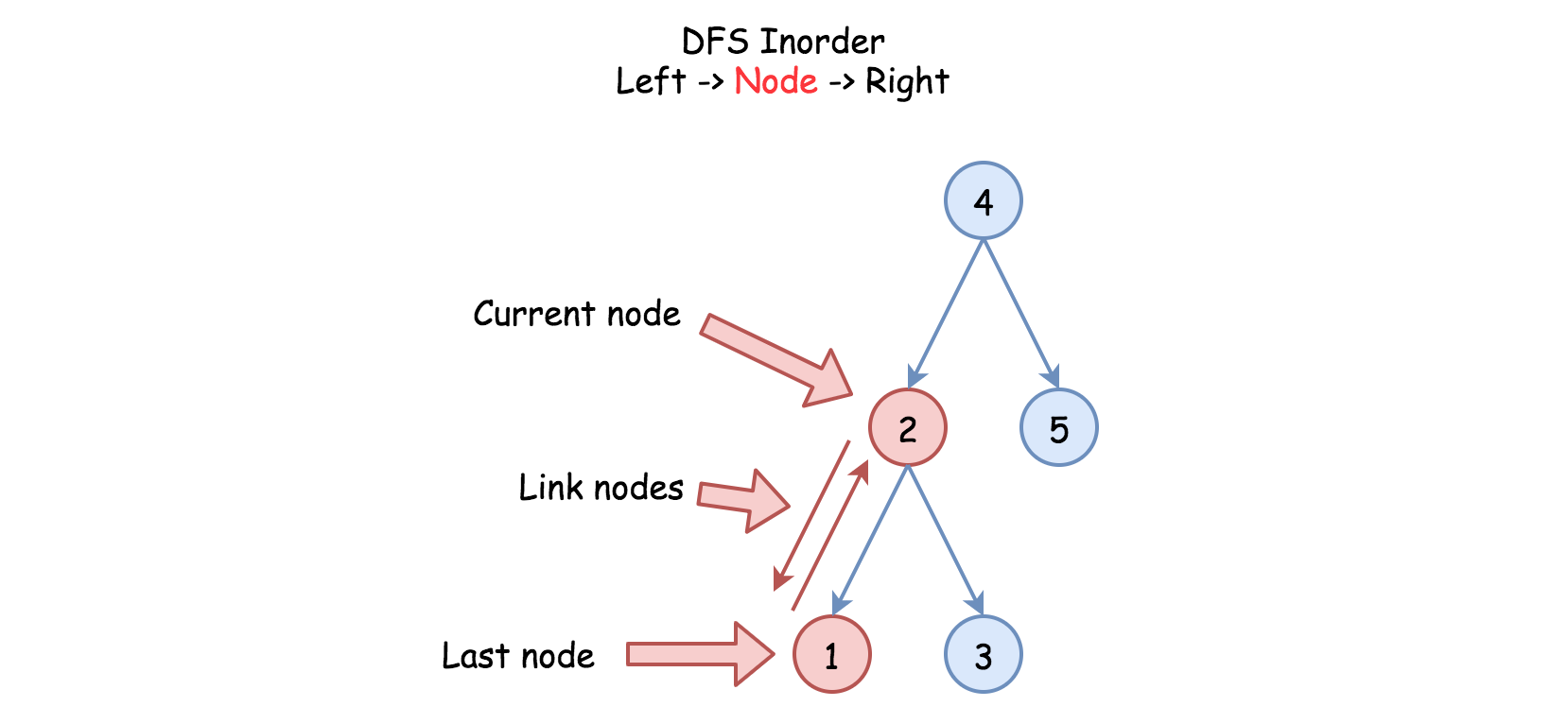
另外一个细节：我们也需要保留第一个，也就是最小的结点，以完成闭环。

下面是具体算法：

将 first 和 last 结点 初始化为 null。

调用标准中序遍历 inOrder(root) :

• 若结点不为 null :
• 调用左子树递归 inOrder(node.left)。
• 若 last 结点不为空，将 last 与当前的 node 链接。
• 否则初始化 first 结点。
• 将当前结点标记为最后 : last = node.
• 调用右子树递归 inOrder(node.right)。

将最前与最后的结点链接完成闭环，返回 first 。

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/

class Solution {
public:
    Node* first = nullptr;
    Node* last = nullptr;

    Node* treeToDoublyList(Node* root) {
        if (!root) return nullptr;
        inOrder(root);
        first->left = last;
        last->right = first;
        return first;
    }

    void inOrder(Node* node) {
        if (!node) return;

        inOrder(node->left);

        if (last) {
            last->right = node;
            node->left = last;
        } else {
            first = node;
        }
        last = node;

        inOrder(node->right);
    }
};

426. 将二叉搜索树转化为排序的双向链表

原文：https://www.cnblogs.com/fxh0707/p/15073599.html