树的同构
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
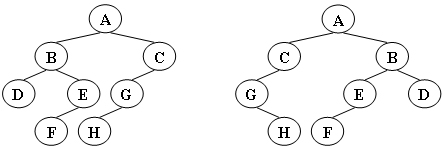
图1
图2
现给定两棵树,请你判断它们是否是同构的。
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N?1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
如果两棵树是同构的,输出“Yes”,否则输出“No”。
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
Yes
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
No
import Foundation
struct TreeNode {
var data: String
var Left: Int?
var Right: Int?
init() {
self.data = "a"
self.Left = nil
self.Right = nil
}
}
var T1 = [TreeNode](repeating: TreeNode.init(), count: 10)
var T2 = [TreeNode](repeating: TreeNode.init(), count: 10)
let null = -1
func Creat(Tree T:inout [TreeNode]) -> Int {
let n = readLine()
let c = Int(n!)!
guard c != 0 else {
return null
}
var root = 0
var data: String
var left: String
var right: String
for i in 0...c-1 {
let word = readLine()!.components(separatedBy: CharacterSet.whitespaces)
data = String(word[0])
T[i].data = data
left = String(word[1])
right = String(word[2])
if left == "-" {
T[i].Left = null
}else{
T[i].Left = Int(left)
root -= T[i].Left!
}
if right == "-"{
T[i].Right = null
}else{
T[i].Right = Int(right)
root -= T[i].Right!
}
root += i
}
return root
}
func judge(R1: Int, R2: Int) -> Bool{
if(R1 == null && R2 == null){
return true
}
if(R1 != null && R2 == null || R1 == null && R2 != null){
return false
}
if(T1[R1].data != T2[R2].data){
return false
}
if (T1[R1].Left != null && T2[R2].Left != null) && (T1[T1[R1].Left!].data == T2[T2[R2].Left!].data){
return judge(R1: T1[R1].Left!, R2: T2[R2].Left!) && judge(R1: T1[R1].Right!, R2: T2[R2].Right!)
}else{
return judge(R1: T1[R1].Left!, R2: T2[R2].Right!) && judge(R1: T1[R1].Right!, R2: T2[R2].Left!)
}
}
var R1 = Creat(Tree: &T1)
var R2 = Creat(Tree: &T2)
let res = judge(R1: R1, R2: R2)
if res {
print("Yes")
}else{
print("No")
}
以上为Swift的判断树同构
原文:https://www.cnblogs.com/Transirizo/p/15087499.html