一维卷积过程理解及代码

以一个例子展示一维卷积过程：

原理

假设输入数据为 6 个维度的数据，有 4 个通道，即[6,4]的数据。
设置核大小（kernel_size）为 2，卷积的步长（stride）为 2，核数量（也就是out_channels）为 1 的卷积。
其中卷积核的通道数和输入的通道数相同，即同样是 4 。
卷积过程及结果如下图所示：

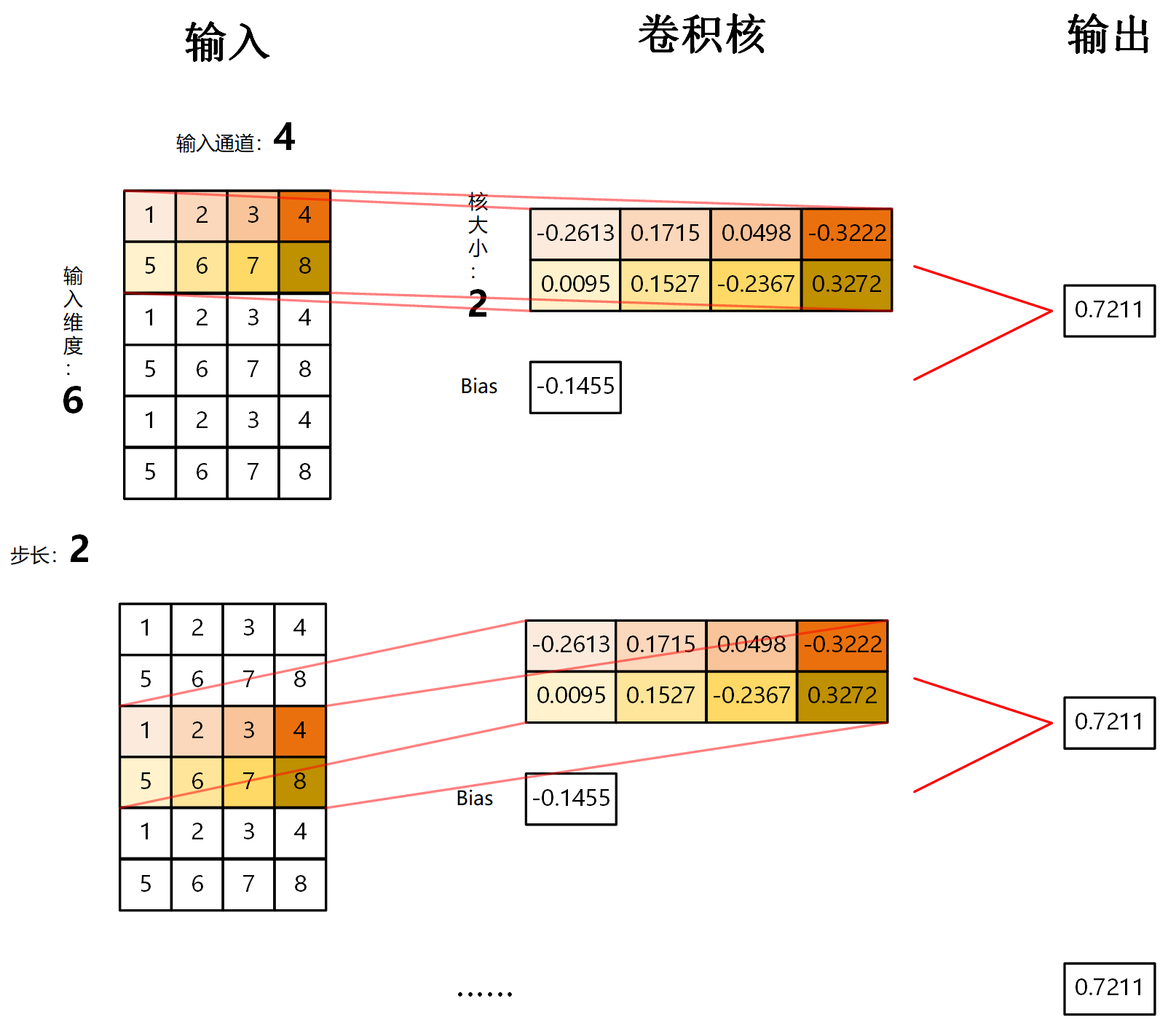
得到一个[1,3]得输出。
第一维结果1：由于核维度默认和输入通道数相同，所以当只有一个卷积核时，第一维输出就为1。有多少个卷积核，输出第一维就是多少。
第二维结果3：可通过公式计算：\(N=\frac{W-F+2P}{S}+1\)。其中：\(W\)为输入大小，\(F\)为核大小，\(P\)为填充大小，\(S\)为步长。

代码

通过pytorch的实现：
pytorch的一维卷积nn.Conv1d()参数：

• in_channels (int) – Number of channels in the input image
• out_channels (int) – Number of channels produced by the convolution
• kernel_size (int or tuple) – Size of the convolving kernel
• stride (int or tuple, optional) – Stride of the convolution. Default: 1
• padding (int, tuple or str, optional) – Padding added to both sides of the input. Default: 0
• padding_mode (string, optional) – ‘zeros‘, ‘reflect‘, ‘replicate‘ or ‘circular‘. Default: ‘zeros‘
• dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
• groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
• bias (bool, optional) – If True, adds a learnable bias to the output. Default: True

例程：

import torch
import torch.nn as nn

torch.manual_seed(2021)

a = [1, 2, 3, 4]
b = [5, 6, 7, 8]
inp = torch.Tensor([a, b, a, b, a, b])
# 扩充一维，作为batch_size
inp = inp.unsqueeze(0)  
print(inp.shape)
# 调换位置
inp = inp.permute(0, 2, 1)

model = nn.Conv1d(in_channels=4, out_channels=1, kernel_size=2, stride=2, padding=0)
# 显示权重
for name, parameters in model.named_parameters():
    print(name, ‘:‘, parameters)
out = model(inp)

print(out.shape)
print(out)

结果：

NOTE:

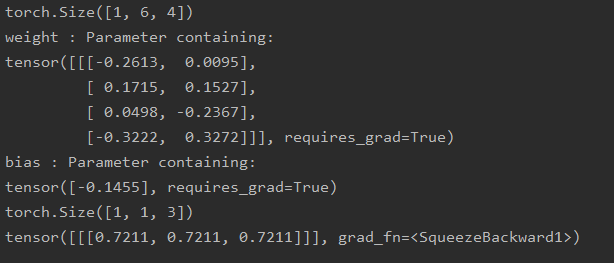
1. 例子里只使用1个数据，即batch_size=1。所以构造了[1, 6, 4]的Tensor，如果一个batch的输入数据，即[batch_size, 6, 4]
2. nn.Conv1d()计算时，它的输入格式是[batch_size, in_channels, in_size]，所以要使用permute()函数，把后面两个维度的顺序调换一下！
3. 一维卷积默认的输入数据其实是2维的。如果是1维的输入数据，应该通过unsqueeze()函数，扩充1维。将[batch_size, 6]变为[batch_size, 6, 1]。卷积过程也如下图所示：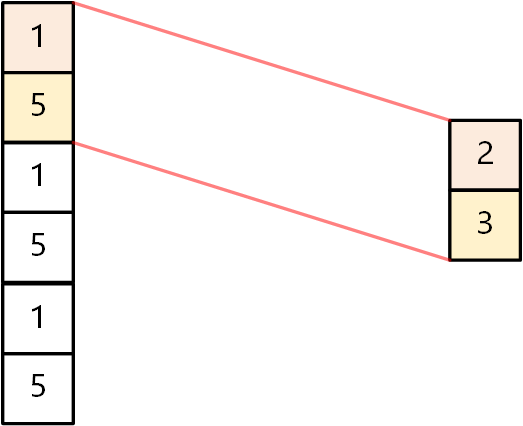

一维卷积过程理解及代码

原文：https://www.cnblogs.com/aionwu/p/15088988.html