归并排序是将两个或两个以上的有序表组合成一个新的有序表。
其基本思想是: 先将 N 个数据看成 N 个长度为 1 的表,将相邻的表成对合并,得到长度为 2 的 N/2 个有序表,进一步将相邻的合并,得到长度为 4 的 N/4 个有序表,以此类推,直到所有数据均合并成一个长度为 N 的有序表为止。每一次归并过程称做一趟。
分解方式分为“从上往下”和“从下往上”两种方式。如下图所示:
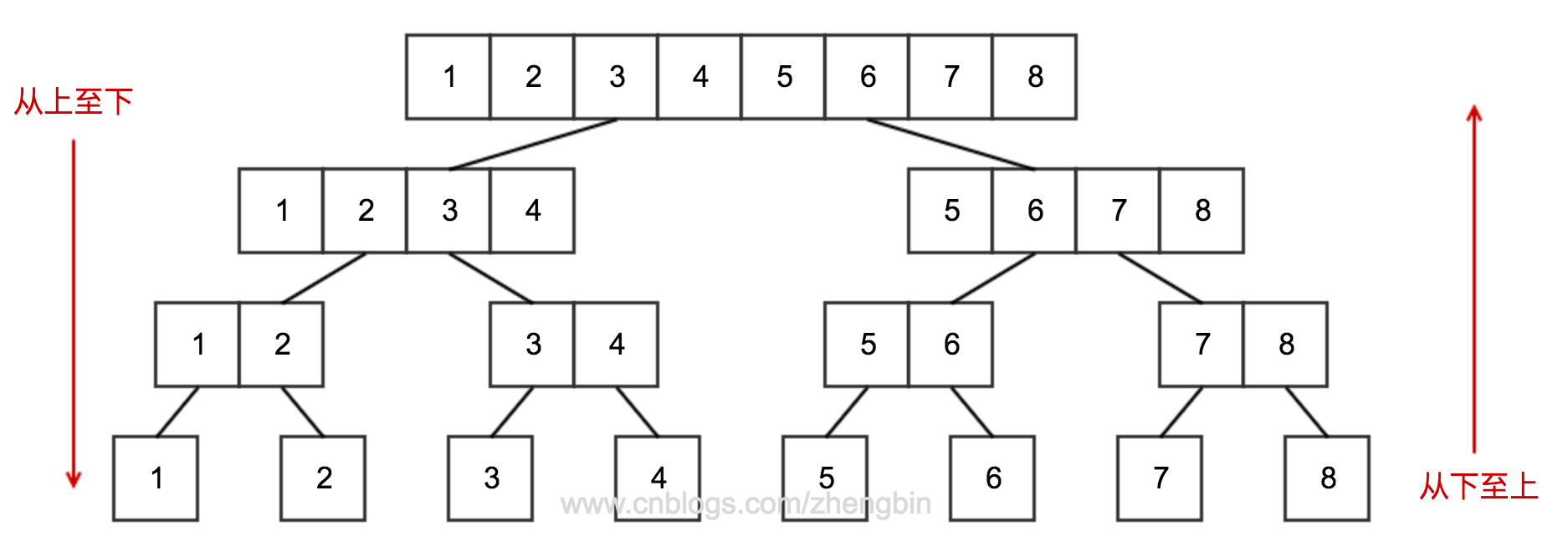
分解:将当前空间一分为二,即求分裂点 mid=(left+right)/2;
求解:递归地对两个子区间 a[left...mid]和 a[mid+1...right]进行归并排序。递归的结束条件为子区间长度为 1(或left>=right)。
/**
* 归并排序 ,从上往下(递归)
* @param arr 需要排序的数组
* @param left 左节点
* @param right 右节点
*/
public void mergeSort1(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int mid = (left + right) / 2;
// 左边
mergeSort1(arr,left,mid);
// 右边
mergeSort1(arr, mid + 1, right);
// 合并
mergeArr(arr, left, mid, right);
}
将待排序的数列分成若干个长度为 1 的子数列,然后将这些数列两两合并;得到若干个长度为 2 的有序数列,再将这些数列两两合并,得到长度为 4 的有序数列,直到合并成一个完整数列为止。这就得到了我们想要的排序结果
/**
* 归并排序 ,从下往上(非递归)
*
* @param arr 需要排序的数组
*/
public void mergeSort2(int[] arr) {
if (null == arr || arr.length < 2) {
return;
}
// 每组的个数
int mergeSize = 1;
int N = arr.length;
while (mergeSize < N) {
int l = 0;
while (l < N) {
int m = l + mergeSize - 1;
while (m >= N) {
break;
}
int R = Math.min(m + mergeSize, N - 1);
mergeArr(arr, l, m, R);
l = R + 1;
}
// 越界处理,一般情况不会出现
if (mergeSize > N / 2) {
break;
}
mergeSize <<= 1;
}
}
将两个子区间 arr[low...mid]和 arr[mid+1...high]归并为一个有序的区间 arr[low...high]。
在归并的过程中需要申请一个临时数组空间,将待排序的两数组顺序的保存在该临时空间中。最后将有序的临时空间覆盖到原数组中。此时数组就变为局部有序了。
/**
* 合并左右两个区间数组
* @param arr
* @param left
* @param mid
* @param right
*/
public void mergeArr(int[] arr, int left, int mid, int right) {
// 临时的数组
int[] temp = new int[right - left + 1];
int tempIndex = 0;
int p1 = left;
int p2 = mid + 1;
// p1 和p2 不越界的情况下
while (p1 <= mid && p2 <= right) {
temp[tempIndex++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
// 拷贝p1剩下部分
while (p1 <= mid) {
temp[tempIndex++] = arr[p1++];
}
// 拷贝p1剩下部分
while (p2 <= right) {
temp[tempIndex++] = arr[p2++];
}
// 将这部分排好序的部分刷入
for (int i = 0; i < temp.length; i++) {
arr[left + i] = temp[i];
}
}
归并排序的时间复杂度是O(nlgn)。
归并排序的形式就是二叉树,需要遍历的次数就是二叉树的深度,根据完全二叉树的性质,其深度为lgn,则得出时间复杂度为O(n*lgn)。
public class MergeSortDemo1 {
/**
* 归并排序 ,从上往下(递归)
* @param arr 需要排序的数组
* @param left 左节点
* @param right 右节点
*/
public void mergeSort1(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int mid = (left + right) / 2;
// 左边
mergeSort1(arr,left,mid);
// 右边
mergeSort1(arr, mid + 1, right);
// 合并
mergeArr(arr, left, mid, right);
}
/**
* 归并排序 ,从下往上(非递归)
*
* @param arr 需要排序的数组
*/
public void mergeSort2(int[] arr) {
if (null == arr || arr.length < 2) {
return;
}
// 每组的个数
int mergeSize = 1;
int N = arr.length;
while (mergeSize < N) {
int l = 0;
while (l < N) {
int m = l + mergeSize - 1;
while (m >= N) {
break;
}
int R = Math.min(m + mergeSize, N - 1);
mergeArr(arr, l, m, R);
l = R + 1;
}
// 越界处理,一般情况不会出现
if (mergeSize > N / 2) {
break;
}
mergeSize <<= 1;
}
}
/**
* 合并左右两个区间数组
* @param arr
* @param left
* @param mid
* @param right
*/
public void mergeArr(int[] arr, int left, int mid, int right) {
// 临时的数组
int[] temp = new int[right - left + 1];
int tempIndex = 0;
int p1 = left;
int p2 = mid + 1;
// p1 和p2 不越界的情况下
while (p1 <= mid && p2 <= right) {
temp[tempIndex++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
// 拷贝p1剩下部分
while (p1 <= mid) {
temp[tempIndex++] = arr[p1++];
}
// 拷贝p1剩下部分
while (p2 <= right) {
temp[tempIndex++] = arr[p2++];
}
// 将这部分排好序的部分刷入
for (int i = 0; i < temp.length; i++) {
arr[left + i] = temp[i];
}
}
private void sort1(int[] arr) {
mergeSort1(arr, 0, arr.length - 1);
}
private void sort2(int[] arr) {
mergeSort2(arr);
}
@Test
public void testMergeSort1() {
int[] arr = {11, 7, 2,11, 9, 8, 18};
sort1(arr);
for (int i : arr) {
System.out.print(i+" ");
}
}
@Test
public void testMergeSort2() {
int[] arr = {11, 7, 2,11, 9, 8, 18};
sort2(arr);
for (int i : arr) {
System.out.print(i+" ");
}
}
}
原文:https://www.cnblogs.com/wuzhixuan/p/15091962.html