1 前言
在 前面的博客 CRC校验原理和verilog实现方法(一) 中,介绍了CRC校验的原理和手动计算过程。本文说一下我在学习CRC校验FPGA实现的一点心得体会。
2 线性反馈移位寄存器
线性反馈移位寄存器简称LFSR,用于产生可重复的伪随机序列,也可用来实现CRC校验。LFSR主要由触发器(寄存器)、异或门以及反馈线路组成。
已知多项式![]() ,其中gn~g0 是系数,g0取值为1,其他系数可以是0或1。该多项式用二进制表示为
,其中gn~g0 是系数,g0取值为1,其他系数可以是0或1。该多项式用二进制表示为![]() ,用LFSR表示为:
,用LFSR表示为:
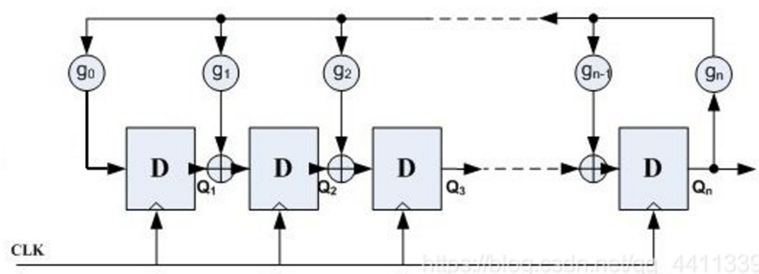
或者表示为:
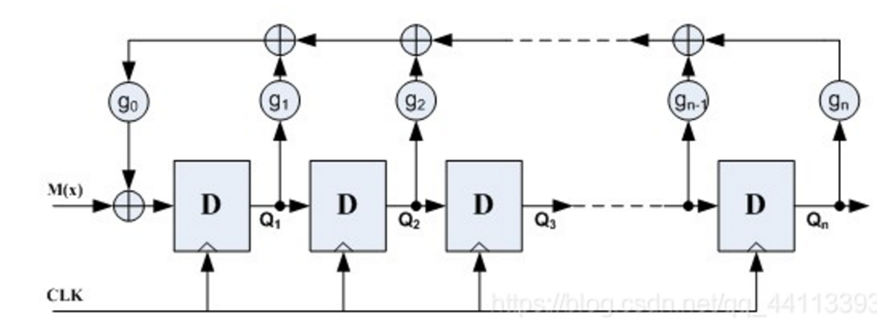
第一种表示法为伽罗瓦LFSR,第二种表示法叫斐波那契LFSR。
可以看出,对于一个n次多项式,可以使用n-1个移位寄存器和最多n-2个异或门实现。LFSR可以实现模二除法。
3 模2除法与LFSR
把被除数的数据,从第一个寄存器的输入端接入,就可以实现模二运算。
对于一个n次多项式,可以使用n-1个移位寄存器,和最多n-1个异或门,实现模二运算。
假如被除数是2位的数据S[1:0]=01b,多项式是10011b。在CRC校验里面,习惯省略最高位的1,多项式用0011b表示。那么S除以0011b的模二运算数字电路结构为:
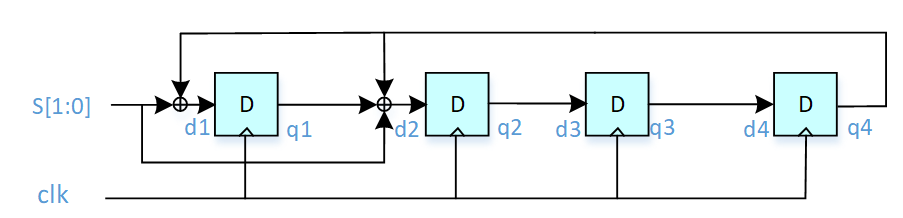
其中d1~d4是寄存器输入;q1~q4是寄存器输出。寄存器需要赋初值,一般赋全1或全0。
下面对模二运算的逻辑表达式进行推导。
首先MSB参与计算,此时:
d1=S[1]^q4;
d2= S[1]^q1^q4;
d3=q2;
d4=q3。
经过一次移位后:
q1=d1= S[1]^q4;
q2= d2= S[1]^q1^q4;
q3= d3=q2;
q4= d4=q3。
此时有:
d1=S[0]^q3;
d2= S[0]^ S[1]^q4^q3;
d3= S[1]^q1^q4;
d4= q2。
令c[3:0]={q4,q3,q2,q1},d[3:0]={d4,d3,d2,d1},那么d就是最终的运算结果表达式,如下
d[3]=c[1];
d[2]= S[1]^c[0]^c[3];
d[1]= S[0]^ S[1]^ c[3]^ c[2];
d[0]= S[0]^ c[2]。
令c的初值为0,则01b对0011b的模二除法的余数为0011。
与手动计算进行对比,结果一致。
上述的被除数S可以换成任意位宽,推导过程一样,当然S位宽越大,推导越复杂,最终的逻辑表达式也越复杂。
上面的逻辑表达式,用verilog异或逻辑门很容易实现。
4 CRC校验的verilog实现
知道如何用verilog实现模二除法,CRC校验的实现就很容易了。但是CRC校验模型一般会有一些特定要求,如输入输出翻转、CRC寄存器初始值等。下一篇博客继续分享。
参考链接:
1、 https://blog.csdn.net/qq_44113393/article/details/89852994
2、 https://www.cnblogs.com/weijianlong/p/11947741.html
原文:https://www.cnblogs.com/y0011/p/15076764.html