















/*
* 程序名:seqstack3.c,此程序演示用顺序栈实现中缀表达式转后缀表达式。
* 作者:C语言技术网(www.freecplus.net) 日期:20201230
*/
#include <stdio.h>
#include <string.h>
#define MAXSIZE 100 // 顺序栈的最大长度。 // xxxxx
typedef char ElemType; // 自定义顺序栈的数据元素为字符。 // xxxx
typedef struct
{
ElemType data[MAXSIZE]; // 用数组存储顺序栈中的元素。
int top; // 栈顶指针,从0到MAXSIZE-1,-1表示空栈。
// 也可以从1到MAXSIZE,0表示空栈。
}SeqStack,*PSeqStack;
// 顺序栈SS的初始化操作。
void InitStack(PSeqStack SS);
// 销毁顺序栈SS。
void DestroyStack(PSeqStack SS);
// 元素入栈,返回值:0-失败;1-成功。
int Push(PSeqStack SS, ElemType *ee);
// 元素出栈,返回值:0-失败;1-成功。
int Pop(PSeqStack SS, ElemType *ee);
// 求顺序栈的长度,返回值:栈SS中元素的个数。
int Length(PSeqStack SS);
// 清空顺序栈。
void Clear(PSeqStack SS);
// 判断顺序栈是否为空,返回值:1-空,0-非空或失败。
int IsEmpty(PSeqStack SS);
// 判断顺序栈是否已满,返回值:1-已满,0-未满或失败。
int IsFull(PSeqStack SS);
// 打印顺序栈中全部的元素。
void PrintStack(PSeqStack SS);
// 获取栈顶元素,返回值:0-失败;1-成功。
// 只查看栈顶元素的值,元素不出栈。
int GetTop(PSeqStack SS, ElemType *ee);
// 把中缀表达式str1转换为后缀表达式str2。
int torpolish(char *str1,char *str2);
int main(int argc,char *argv[])
{
char str1[101],str2[101];
memset(str1,0,sizeof(str1));
memset(str2,0,sizeof(str2));
printf("请输入待转换的表达式:");
fgets(str1,100,stdin); // 不建议用gets函数,gets函数编译时可能会出现警号。
str1[strlen(str1)-1]=0; // 删除str1最后的换行。
printf("输入转换的表达式=%s=\n",str1);
// 把中缀表达式str1转换为后缀表达式str2。
if (torpolish(str1,str2) == 0) { printf("转换失败。\n"); return -1; }
printf("转换成功=%s=。\n",str2);
return 1;
}
// 把中缀表达式str1转换为后缀表达式str2。
int torpolish(char *str1,char *str2)
{
SeqStack SS; // 创建顺序栈。
InitStack(&SS); // 初始化顺序栈。
ElemType ee; // 创建一个数据元素。
int ipos1=0,len=strlen(str1),ipos2=0;
// 从左到右扫描中缀表达式。
for (ipos1=0;ipos1<len;ipos1++)
{
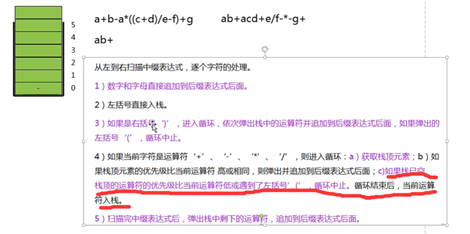
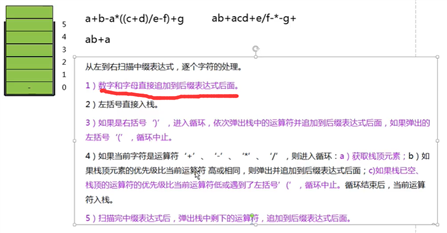
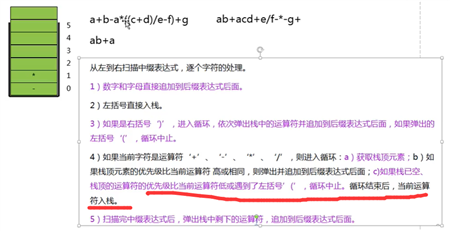
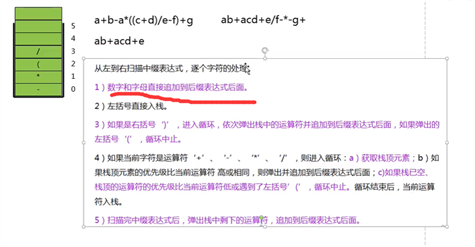
// 数字和字母直接追加到后缀表达式后面。
if ( ( (str1[ipos1]>=‘0‘) && (str1[ipos1]<=‘9‘) ) ||
( (str1[ipos1]>=‘a‘) && (str1[ipos1]<=‘z‘) ) ||
( (str1[ipos1]>=‘A‘) && (str1[ipos1]<=‘Z‘) ) )
{
str2[ipos2]=str1[ipos1]; ipos2++; continue;
}
// 左括号‘(‘直接入栈。
if (str1[ipos1]==‘(‘) { Push(&SS,&str1[ipos1]); continue; }
// 如果是右括号‘)‘,依次弹出栈中的运算符并追加到后缀表达式中,直到出现左括号‘(‘。
if (str1[ipos1]==‘)‘)
{
while (1)
{
// 一定要判断出栈结果,如果栈中没有元素,转换失败(因为没找到左括号‘(‘)。
if ( Pop(&SS,&ee) != 1) return 0;
if ( ee == ‘(‘) break;
str2[ipos2]=ee; ipos2++;
}
continue;
}
// 如果是算术运算符‘+‘、‘-‘、‘*‘、‘/‘。
if ( (str1[ipos1]==‘+‘) || (str1[ipos1]==‘-‘) || (str1[ipos1]==‘*‘) || (str1[ipos1]==‘/‘) )
{
while (1)
{
// 获取栈中运算符,如果栈为空,当前运算符直接入栈。
if (GetTop(&SS,&ee) != 1) break;
if ( ee==‘(‘ ) break; // 如果遇到左括号,停止判断,当前运算符将入栈。
int pri1; // 当前运算符的优先级。
int pri2; // 栈中运算符的优先级。
if ( (str1[ipos1]==‘+‘) || (str1[ipos1]==‘-‘) ) pri1=1;
if ( (str1[ipos1]==‘*‘) || (str1[ipos1]==‘/‘) ) pri1=2;
if ( (ee==‘+‘) || (ee==‘-‘) ) pri2=1;
if ( (ee==‘*‘) || (ee==‘/‘) ) pri2=2;
// 如果当前运算符的优先级 高于 栈中运算符的优先级,停止判断,当前运算符将入栈。
if (pri1>pri2) break;
// 把栈中优先级 高于等于 当前运算符的元素依次弹出,追加到后缀表达式后面。
Pop(&SS,&ee); str2[ipos2]=ee; ipos2++; continue;
}
// 当前运算符入栈。
Push(&SS,&str1[ipos1]);
continue;
}
}
// 弹出栈中其它的运算符,追加到后缀表达式后面。
while (1)
{
if (Pop(&SS,&ee)!=1) break;
str2[ipos2]=ee; ipos2++;
}
return 1;
}
// 初始化顺序栈
void InitStack(PSeqStack SS)
{
Clear(SS); // 清空顺序栈。
}
// 清空顺序栈。
void Clear(PSeqStack SS)
{
if (SS == NULL) return; // 检查空指针。
SS->top=-1; // 栈顶指针置为-1。
memset(SS->data,0,sizeof(ElemType)*MAXSIZE); // 数组元素清零。
}
// 求顺序栈的长度,返回值:栈SS中元素的个数。
int Length(PSeqStack SS)
{
if (SS == NULL) return 0; // 检查空指针。
return SS->top+1;
}
// 销毁顺序栈SS。
void DestroyStack(PSeqStack SS)
{
// 静态顺序栈无需释放内存,不需要销毁操作。
Clear(SS); // 清空顺序栈。
return;
}
// 判断顺序栈是否为空,返回值:1-空,0-非空或失败。
int IsEmpty(PSeqStack SS)
{
if (SS == NULL) return 0; // 检查空指针。
if (SS->top == -1) return 1;
return 0;
}
// 判断顺序栈是否已满,返回值:1-已满,0-未满或失败。
int IsFull(PSeqStack SS)
{
if (SS == NULL) return 0; // 检查空指针。
if (SS->top >= MAXSIZE-1) return 1;
return 0;
}
// 元素入栈,返回值:0-失败;1-成功。
int Push(PSeqStack SS, ElemType *ee)
{
if ( (SS == NULL) || (ee == NULL) ) return 0; // 检查空指针。
if (IsFull(SS) == 1)
{
printf("顺序栈已满,不能插入。\n"); return 0;
}
SS->top++; // 栈指针先加1。
memcpy(&SS->data[SS->top],ee,sizeof(ElemType)); // 用数组的下标访问。
// memcpy(SS->data+SS->top,ee,sizeof(ElemType)); // 采用指针运算也可以。
return 1;
}
// 打印顺序栈中全部的元素。
void PrintStack(PSeqStack SS)
{
if (SS == NULL) return; // 检查空指针。
if (SS->top == -1) { printf("栈为空。\n"); return; }
int kk;
for (kk = 0; kk <= SS->top; kk++)
{
printf("SS[%d],value=%c\n",kk,SS->data[kk]); // 用数组的下标访问。 xxx
// printf("SS[%d],value=%d\n",kk,*(SS->data+kk)); // 采用指针运算也可以。
}
}
// 元素出栈,返回值:0-失败;1-成功。
int Pop(PSeqStack SS, ElemType *ee)
{
if ( (SS == NULL) || (ee == NULL) ) return 0; // 检查空指针。
if (SS->top == -1) { printf("栈为空。\n"); return 0; }
memcpy(ee,&SS->data[SS->top],sizeof(ElemType)); // 用数组的下标访问。
// memcpy(ee,SS->data+SS->top,sizeof(ElemType)); // 采用指针运算也可以。
SS->top--; // 栈指针减1。
return 1;
}
// 获取栈顶元素,返回值:0-失败;1-成功。
// 只查看栈顶元素的值,元素不出栈。
int GetTop(PSeqStack SS, ElemType *ee)
{
if ( (SS == NULL) || (ee == NULL) ) return 0; // 检查空指针。
if (IsEmpty(SS) == 1) { printf("栈为空。\n"); return 0; }
memcpy(ee,&SS->data[SS->top],sizeof(ElemType)); // 用数组的下标访问。
// memcpy(ee,SS->data+SS->top,sizeof(ElemType)); // 采用指针运算也可以。
return 1;
}
原文:https://www.cnblogs.com/lnterpreter/p/15093791.html