原理介绍:
alpha-beta滤波是一种可用于状态估计、数据平滑的滤波器,如果对kalman滤波有了解,就会发现ab滤波的形式和kalman相近,但是其最突出的优点是它不依赖系统的具体模型,因此使用起来更简单。
αβ滤波的αβ是指滤波器中两个可以调整的参数。
滤波方程:
假设一个二阶状态模型,比如车辆的速度v、位置p,光测量与一阶对应,即位置p。
如果滤波周期△T比较小,假设速度v这段时间内保持恒定(加速度为或者变化缓慢),与kalman滤波的一步预测类似,我们可以通过如下方程预测下个时刻系统的位置:
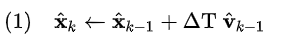
因为假设速度是恒定值,下个时刻的速度与上一个时刻相同:
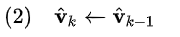
由于方程中并没有考虑噪声和系统的其它动态特性,因此实际的测量值会与上面的预测值不一样,两者之间存在误差r,我们称之为残差或新息。
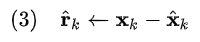
αβ滤波采用选定的α和β常数(滤波器得到其名称),使用偏差r的α倍来矫正位置估计,并使用β乘以偏差r来矫正速度估计,使用ΔT来归一化β的大小。
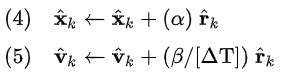
可以将上述的矫正视为沿着梯度下降方向的一小步,随着不断的调整,误差逐渐减小或者消除。
为了保证系统的稳定性,α和β的值必须是一个正值且很小,一般情况下需要满足下式:
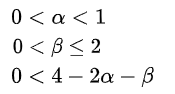
一般通过实验来调整α和β的值,我觉得这是使用 αβ滤波滤波最大的缺点,滤波性能的好坏非常依赖于参数,好在 αβ滤波稳定性比较好,虽然有时得不到很好滤波效果,但是不至于导致发散。
α和β对滤波器的影响如下,还是比较好掌握的,一般花一些时间调试就可以得到比较好的参数
α和β越大,滤波具有更快的动态性能,但是噪声也会加大。α和β越小,噪声越小,滤波后的值更平滑,但是动态性能差。因此需要在动态性能和滤波噪声之间做好平衡。
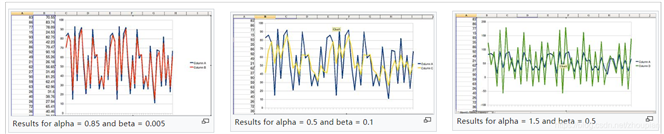
上面三幅图中,蓝色的曲线是原始数据,α和β取不同的值效果会发生明显的变化。
#include <stdio.h> #include <stdlib.h> int main() { float dt = 0.5; float xk_1 = 0, vk_1 = 0, a = 0.85, b = 0.005; float xk, vk, rk; float xm; while( 1 ) { xm = rand() % 100;// input signal xk = xk_1 + ( vk_1 * dt ); vk = vk_1; rk = xm - xk; xk += a * rk; vk += ( b * rk ) / dt; xk_1 = xk; vk_1 = vk; printf( "%f \t %f\n", xm, xk_1 ); sleep( 1 ); } }
如果使用采样间隔T、系统噪声方差

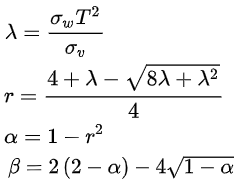
α滤波器只有一个状态量:
![]()
它最优的参数可以通过下面的公式计算

这种滤波本质与滑动平均滤波、低通滤波相同。
当系统的二阶常量变化很快时(加速度很大),可以使用 αβγ滤波,它是对 αβ滤波的一种扩展。在位置x、速度v的基础上引入加速度a,γ用于对加速度进行修正,以下是αβγ滤波的方程。
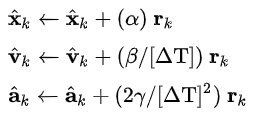
最优的参数计算方法如下。
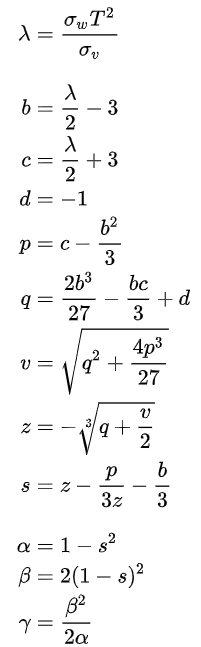
类似,可以将滤波器扩展到更高的阶数,但是大多数高阶系统往往在多个状态之间具有显着的相互作用(不是纯粹的积分环节),此时如果依然将系统近似为积分链就不太合适了。
wiki: https://en.wikipedia.org/wiki/Alpha_beta_filter
原文:https://www.cnblogs.com/gary-guo/p/15102940.html