
pso.m
clc
clear
close all
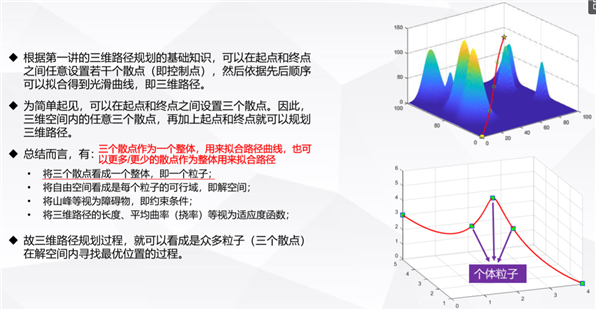
%% 三维路径规划模型定义
startPos = [1, 1, 1];
goalPos = [100, 100, 80];
% 随机定义山峰地图
mapRange = [100,100,100]; % 地图长、宽、高范围
[X,Y,Z] = defMap(mapRange);
%% 初始参数设置
N = 100; % 迭代次数
M = 50; % 粒子数量
pointNum = 3; % 每一个粒子包含三个位置点
w = 1.2; % 惯性权重
c1 = 2; % 社会权重
c2 = 2; % 认知权重
% 粒子位置界限
posBound = [[0,0,0]‘,mapRange‘];
% 粒子速度界限
alpha = 0.1;
velBound(:,2) = alpha*(posBound(:,2) - posBound(:,1));
velBound(:,1) = -velBound(:,2);
%% 种群初始化
% 初始化一个空的粒子结构体
particles.pos= [];
particles.v = [];
particles.fitness = [];
particles.path = [];
particles.Best.pos = [];
particles.Best.fitness = [];
particles.Best.path = [];
% 定义M个粒子的结构体
particles = repmat(particles,M,1);
% 初始化每一代的最优粒子
GlobalBest.fitness = inf;
% 第一代的个体粒子初始化
for i = 1:M
% 粒子按照正态分布随机生成
particles(i).pos.x = unifrnd(posBound(1,1),posBound(1,2),1,pointNum);
particles(i).pos.y = unifrnd(posBound(2,1),posBound(2,2),1,pointNum);
particles(i).pos.z = unifrnd(posBound(3,1),posBound(3,2),1,pointNum);
% 初始化速度
particles(i).v.x = zeros(1, pointNum);
particles(i).v.y = zeros(1, pointNum);
particles(i).v.z = zeros(1, pointNum);
% 适应度
[flag,fitness,path] = calFitness(startPos, goalPos,X,Y,Z, particles(i).pos);
% 碰撞检测判断
if flag == 1
% 若flag=1,表明此路径将与障碍物相交,则增大适应度值
particles(i).fitness = 1000*fitness;
particles(i).path = path;
else
% 否则,表明可以选择此路径
particles(i).fitness = fitness;
particles(i).path = path;
end
% 更新个体粒子的最优
particles(i).Best.pos = particles(i).pos;
particles(i).Best.fitness = particles(i).fitness;
particles(i).Best.path = particles(i).path;
% 更新全局最优
if particles(i).Best.fitness < GlobalBest.fitness
GlobalBest = particles(i).Best;
end
end
% 初始化每一代的最优适应度,用于画适应度迭代图
fitness_beat_iters = zeros(N,1);
%% 循环
for iter = 1:N
for i = 1:M
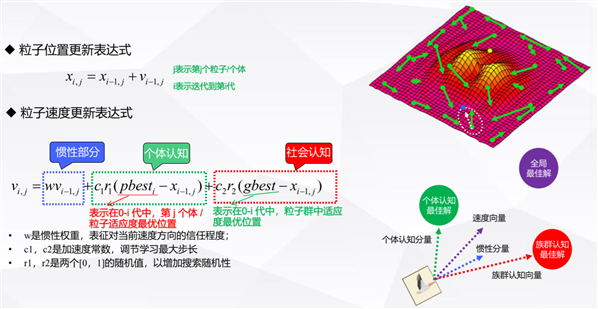
% 更新速度
particles(i).v.x = w*particles(i).v.x ...
+ c1*rand([1,pointNum]).*(particles(i).Best.pos.x-particles(i).pos.x) ...
+ c2*rand([1,pointNum]).*(GlobalBest.pos.x-particles(i).pos.x);
particles(i).v.y = w*particles(i).v.y ...
+ c1*rand([1,pointNum]).*(particles(i).Best.pos.y-particles(i).pos.y) ...
+ c2*rand([1,pointNum]).*(GlobalBest.pos.y-particles(i).pos.y);
particles(i).v.z = w*particles(i).v.z ...
+ c1*rand([1,pointNum]).*(particles(i).Best.pos.z-particles(i).pos.z) ...
+ c2*rand([1,pointNum]).*(GlobalBest.pos.z-particles(i).pos.z);
% 判断是否位于速度界限以内
particles(i).v.x = min(particles(i).v.x, velBound(1,2));
particles(i).v.x = max(particles(i).v.x, velBound(1,1));
particles(i).v.y = min(particles(i).v.y, velBound(2,2));
particles(i).v.y = max(particles(i).v.y, velBound(2,1));
particles(i).v.z = min(particles(i).v.z, velBound(3,2));
particles(i).v.z = max(particles(i).v.z, velBound(3,1));
% 更新粒子位置
particles(i).pos.x = particles(i).pos.x + particles(i).v.x;
particles(i).pos.y = particles(i).pos.y + particles(i).v.y;
particles(i).pos.z = particles(i).pos.z + particles(i).v.z;
% 判断是否位于粒子位置界限以内
particles(i).pos.x = max(particles(i).pos.x, posBound(1,1));
particles(i).pos.x = min(particles(i).pos.x, posBound(1,2));
particles(i).pos.y = max(particles(i).pos.y, posBound(2,1));
particles(i).pos.y = min(particles(i).pos.y, posBound(2,2));
particles(i).pos.z = max(particles(i).pos.z, posBound(3,1));
particles(i).pos.z = min(particles(i).pos.z, posBound(3,2));
% 适应度计算
[flag,fitness,path] = calFitness(startPos, goalPos,X,Y,Z, particles(i).pos);
% 碰撞检测判断
if flag == 1
% 若flag=1,表明此路径将与障碍物相交,则增大适应度值
particles(i).fitness = 1000*fitness;
particles(i).path = path;
else
% 否则,表明可以选择此路径
particles(i).fitness = fitness;
particles(i).path = path;
end
% 更新个体粒子最优
if particles(i).fitness < particles(i).Best.fitness
particles(i).Best.pos = particles(i).pos;
particles(i).Best.fitness = particles(i).fitness;
particles(i).Best.path = particles(i).path;
% 更新全局最优粒子
if particles(i).Best.fitness < GlobalBest.fitness
GlobalBest = particles(i).Best;
end
end
end
% 把每一代的最优粒子赋值给fitness_beat_iters
fitness_beat_iters(iter) = GlobalBest.fitness;
% 在命令行窗口显示每一代的信息
disp([‘第‘ num2str(iter) ‘代:‘ ‘最优适应度 = ‘ num2str(fitness_beat_iters(iter))]);
% 画图
plotFigure(startPos,goalPos,X,Y,Z,GlobalBest);
pause(0.001);
end
%% 结果展示
% 理论最小适应度:直线距离
fitness_best = norm(startPos - goalPos);
disp([ ‘理论最优适应度 = ‘ num2str(fitness_best)]);
% 画适应度迭代图
figure
plot(fitness_beat_iters,‘LineWidth‘,2);
xlabel(‘迭代次数‘);
ylabel(‘最优适应度‘);
calFitness.m
function [flag,fitness,path] = calFitness(startPos, goalPos,X,Y,Z, pos)
% 利用三次样条拟合散点
x_seq=[startPos(1), pos.x, goalPos(1)];
y_seq=[startPos(2), pos.y, goalPos(2)];
z_seq=[startPos(3), pos.z, goalPos(3)];
k = length(x_seq);
i_seq = linspace(0,1,k);
I_seq = linspace(0,1,100);
X_seq = spline(i_seq,x_seq,I_seq);
Y_seq = spline(i_seq,y_seq,I_seq);
Z_seq = spline(i_seq,z_seq,I_seq);
path = [X_seq‘, Y_seq‘, Z_seq‘];
% 判断生成的曲线是否与与障碍物相交
flag = 0;
for i = 2:size(path,1)
x = path(i,1);
y = path(i,2);
z_interp = interp2(X,Y,Z,x,y);
if path(i,3) < z_interp
flag = 1;
break
end
end
%% 计算三次样条得到的离散点的路径长度(适应度)
dx = diff(X_seq);
dy = diff(Y_seq);
dz = diff(Z_seq);
fitness = sum(sqrt(dx.^2 + dy.^2 + dz.^2));
图像结果
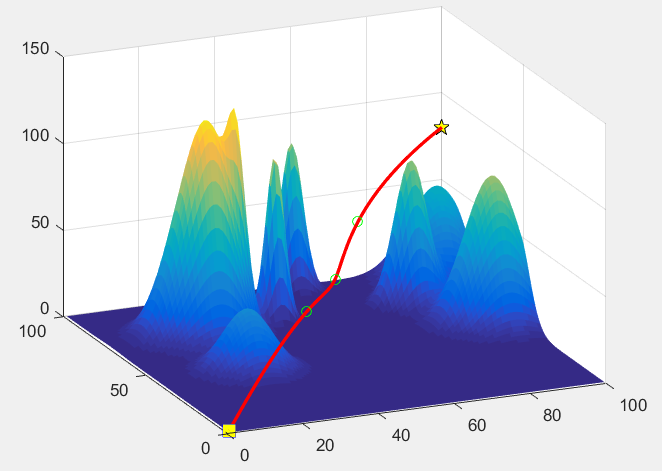
原文:https://www.cnblogs.com/zhjblogs/p/15111492.html