
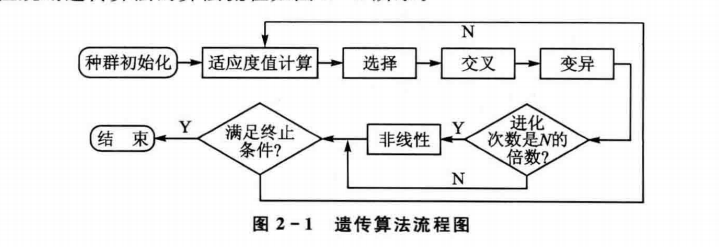
函数fmincon是Matlab最优化工具箱中求解非线性规划问题的函数,它从一个预估值出发,搜索约束条件下非线性多元函数的最小值。
fmincon函数的约束条件如下:
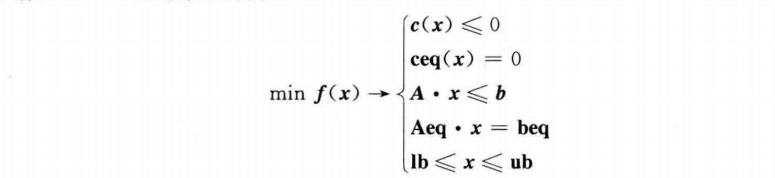
其中,\(x\),\(b,beq,lb\)和\(ub\)是矢量;\(A\)和\(Aeq\)为矩阵;\(c(x)\)和\(ceq(x)\)返回矢量的函数;\(f(x),c(x)\)和\(ceq(x)\)是非线性函数。


其中,nonlcon为非线性约束条件;lb和ub分别为x的下界和上界。








function y = fun(x)
y=-5*sin(x(1))*sin(x(2))*sin(x(3))*sin(x(4))*sin(x(5))-sin(5*x(1))*sin(5*x(2))*sin(5*x(3))*sin(5*x(4))*sin(5*x(5))+8;
%% 清空环境
clc
clear
warning off
%% 遗传算法参数
maxgen=30; %进化代数
sizepop=100; %种群规模
pcross=[0.6]; %交叉概率
pmutation=[0.01]; %变异概率
lenchrom=[1 1 1 1 1]; %变量字串长度
bound=[0 0.9*pi;0 0.9*pi;0 0.9*pi;0 0.9*pi;0 0.9*pi]; %变量范围
%% 个体初始化
individuals=struct(‘fitness‘,zeros(1,sizepop), ‘chrom‘,[]); %种群结构体
avgfitness=[]; %种群平均适应度
bestfitness=[]; %种群最佳适应度
bestchrom=[]; %适应度最好染色体
% 初始化种群
for i=1:sizepop
individuals.chrom(i,:)=Code(lenchrom,bound); %随机产生个体
x=individuals.chrom(i,:);
individuals.fitness(i)=fun(x); %个体适应度
end
%找最好的染色体
[bestfitness bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:); %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[];
%% 进化开始
for i=1:maxgen
% 选择操作
individuals=Select(individuals,sizepop);
avgfitness=sum(individuals.fitness)/sizepop;
% 交叉操作
individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
% 变异操作
individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,[i maxgen],bound);
if mod(i,10)==0
individuals.chrom=nonlinear(individuals.chrom,sizepop);
end
% 计算适应度
for j=1:sizepop
x=individuals.chrom(j,:);
individuals.fitness(j)=fun(x);
end
%找到最小和最大适应度的染色体及它们在种群中的位置
[newbestfitness,newbestindex]=min(individuals.fitness);
[worestfitness,worestindex]=max(individuals.fitness);
% 代替上一次进化中最好的染色体
if bestfitness>newbestfitness
bestfitness=newbestfitness;
bestchrom=individuals.chrom(newbestindex,:);
end
individuals.chrom(worestindex,:)=bestchrom;
individuals.fitness(worestindex)=bestfitness;
avgfitness=sum(individuals.fitness)/sizepop;
trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%进化结束
%% 结果显示
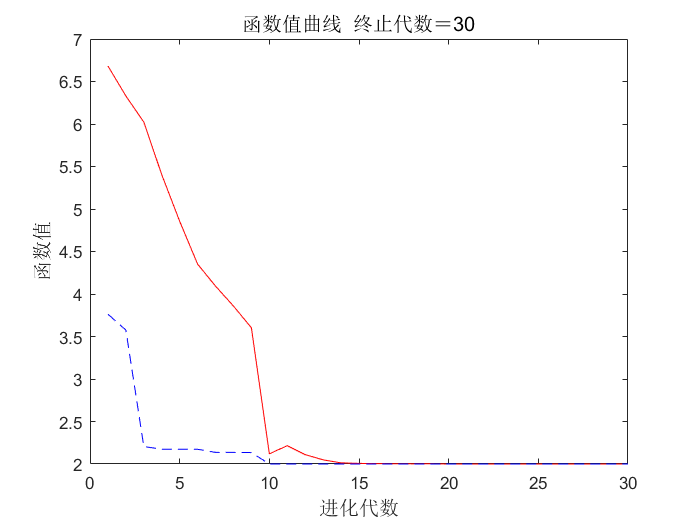
figure
[r c]=size(trace);
plot([1:r]‘,trace(:,1),‘r-‘,[1:r]‘,trace(:,2),‘b--‘);
title([‘函数值曲线 ‘ ‘终止代数=‘ num2str(maxgen)],‘fontsize‘,12);
xlabel(‘进化代数‘,‘fontsize‘,12);ylabel(‘函数值‘,‘fontsize‘,12);
legend(‘各代平均值‘,‘各代最佳值‘,‘fontsize‘,12);
ylim([1.5 8])
disp(‘函数值 变量‘);
% 窗口显示
disp([bestfitness x]);
grid on
function ret=Select(individuals,sizepop)
% 本函数对每一代种群中的染色体进行选择,以进行后面的交叉和变异
% individuals input : 种群信息
% sizepop input : 种群规模
% opts input : 选择方法的选择
% ret output : 经过选择后的种群
individuals.fitness= 1./(individuals.fitness);
sumfitness=sum(individuals.fitness);
sumf=individuals.fitness./sumfitness;
index=[];
for i=1:sizepop %转sizepop次轮盘
pick=rand;
while pick==0
pick=rand;
end
for j=1:sizepop
pick=pick-sumf(j);
if pick<0
index=[index j];
break; %寻找落入的区间,此次转轮盘选中了染色体i,注意:在转sizepop次轮盘的过程中,有可能会重复选择某些染色体
end
end
end
individuals.chrom=individuals.chrom(index,:);
individuals.fitness=individuals.fitness(index);
ret=individuals;
function ret=Cross(pcross,lenchrom,chrom,sizepop,bound)
%本函数完成交叉操作
% pcorss input : 交叉概率
% lenchrom input : 染色体的长度
% chrom input : 染色体群
% sizepop input : 种群规模
% ret output : 交叉后的染色体
for i=1:sizepop
% 随机选择两个染色体进行交叉
pick=rand(1,2);
while prod(pick)==0
pick=rand(1,2);
end
index=ceil(pick.*sizepop);
% 交叉概率决定是否进行交叉
pick=rand;
while pick==0
pick=rand;
end
if pick>pcross
continue;
end
flag=0;
while flag==0
% 随机选择交叉位置
pick=rand;
while pick==0
pick=rand;
end
pos=ceil(pick.*sum(lenchrom)); %随机选择进行交叉的位置,即选择第几个变量进行交叉,注意:两个染色体交叉的位置相同
pick=rand; %交叉开始
v1=chrom(index(1),pos);
v2=chrom(index(2),pos);
chrom(index(1),pos)=pick*v2+(1-pick)*v1;
chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束
flag1=test(lenchrom,bound,chrom(index(1),:)); %检验染色体1的可行性
flag2=test(lenchrom,bound,chrom(index(2),:)); %检验染色体2的可行性
if flag1*flag2==0
flag=0;
else flag=1;
end %如果两个染色体不是都可行,则重新交叉
end
end
ret=chrom;
function ret=Mutation(pmutation,lenchrom,chrom,sizepop,pop,bound)
% 本函数完成变异操作
% pcorss input : 变异概率
% lenchrom input : 染色体长度
% chrom input : 染色体群
% sizepop input : 种群规模
% pop input : 当前种群的进化代数和最大的进化代数信息
% ret output : 变异后的染色体
for i=1:sizepop
% 随机选择一个染色体进行变异
pick=rand;
while pick==0
pick=rand;
end
index=ceil(pick*sizepop);
% 变异概率决定该轮循环是否进行变异
pick=rand;
if pick>pmutation
continue;
end
flag=0;
while flag==0
% 变异位置
pick=rand;
while pick==0
pick=rand;
end
pos=ceil(pick*sum(lenchrom)); %随机选择了染色体变异的位置,即选择了第pos个变量进行变异
v=chrom(i,pos);
v1=v-bound(pos,1);
v2=bound(pos,2)-v;
pick=rand; %变异开始
if pick>0.5
delta=v2*(1-pick^((1-pop(1)/pop(2))^2));
chrom(i,pos)=v+delta;
else
delta=v1*(1-pick^((1-pop(1)/pop(2))^2));
chrom(i,pos)=v-delta;
end %变异结束
flag=test(lenchrom,bound,chrom(i,:)); %检验染色体的可行性
end
end
ret=chrom;
function ret = nonlinear(chrom,sizepop)
for i=1:sizepop
x=fmincon(inline(‘-5*sin(x(1))*sin(x(2))*sin(x(3))*sin(x(4))*sin(x(5))-sin(5*x(1))*sin(5*x(2))*sin(5*x(3))*sin(5*x(4))*sin(5*x(5))‘),chrom(i,:)‘,[],[],[],[],[0 0 0 0 0],[2.8274 2.8274 2.8274 2.8274 2.8274]);
ret(i,:)=x‘;
end


想详细研究BP神经网络的可以参考:
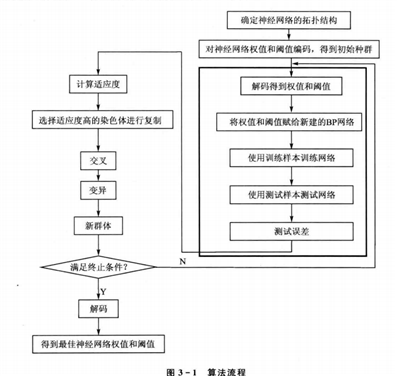
遗传算法优化BP神经网络主要分为:BP神经网络结构确定、遗传算法优化权值和阈值、BP神经网络训练及预测。其中BP神经网络的拓扑结构(可以理解为一种脚手架结构)是根据样本的输入/输出参数个数确定的,这样就可以确定遗传算法优化参数的个数,从而确定种群个体的编码长度。因为遗传算法的优化参数是BP神经网络的初始权值和阈值,只要网络结构已知,权值和阈值的个数就已知了。

1.网络创建
BP网络结构的确定有以下两条比较重要的指导原则。
①对于一般的模式识别问题,三层网络可以很好地解决问题
②在三层网络中,隐含层神经元网络个数\(n_2\)和输入层神经元个数\(n_1\)之间有近似关系:
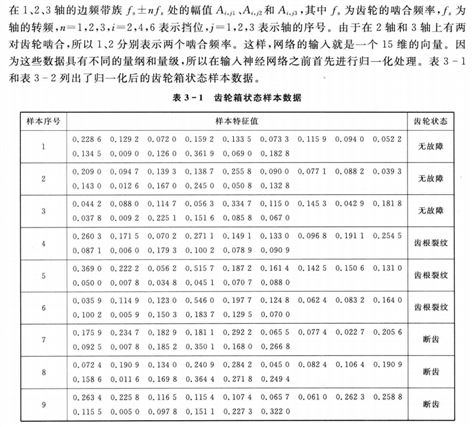
本案例中,由于样本有15个输入参数,3个输出参数,所以\(n_2\)取值为31,设置的BP网络结构为15-31-3,即输入层15个节点,隐含层31个节点,输出层3个节点,共有\(15×31+31×3=558\)个权值,31+3=34个阈值,所以遗传算法优化参数的个数为558+34=592.
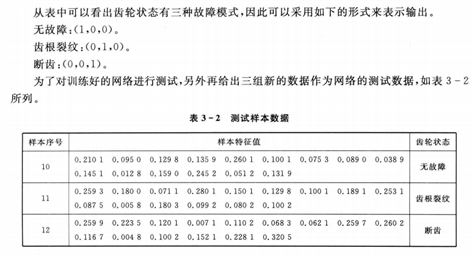
使用表3-1的样本作为训练数据,表3-2中的3个样本作为测试数据。把测试样本的测试误差的范数作为衡量网络的泛化能力(应用到广泛数据中的优劣)再通过误差范数计算个体的适应度值,个体的误差范数越小,个体适应度值越大,该个体越优。
神经网络的隐含层神经元的传递函数采用S型正切函数tansig()【S型函数_百度百科 (baidu.com)】,常用的神经网络激活函数。
net = feedforwardnet(31)
net.layers{2}.transferFcn = ‘logsig‘
(2)网络训练和测试
网络训练是一个不断修正权值和阈值的过程,通过训练,使得网络的输出误差越来越小。在默认情况下,BP神经网络的训练函数为trainlm,具体的网络参数设置及训练代码如下。
%%训练次数为1000,训练目标为0.01,学习速率为0.1
net.trainParam.epochs=1000;
net.trainParam.goal=0.01;
net.trainParam.lr=0.1;
%%训练网络以及测试网络
net=train(net,P,T);
测试,测试样本数据矩阵为P_test,代码如下:
Y = sim(net,P_test)



function err=Bpfun(x,P,T,hiddennum,P_test,T_test)
%% 训练&测试BP网络
%% 输入
% x:一个个体的初始权值和阈值
% P:训练样本输入
% T:训练样本输出
% hiddennum:隐含层神经元数
% P_test:测试样本输入
% T_test:测试样本期望输出
%% 输出
% err:预测样本的预测误差的范数
inputnum=size(P,1); % 输入层神经元个数
outputnum=size(T,1); % 输出层神经元个数
%% 新建BP网络
net=newff(minmax(P),[hiddennum,outputnum],{‘tansig‘,‘logsig‘},‘trainlm‘);
%% 设置网络参数:训练次数为1000,训练目标为0.01,学习速率为0.1
net.trainParam.epochs=1000;
net.trainParam.goal=0.01;
LP.lr=0.1;
net.trainParam.show=NaN;
% net.trainParam.showwindow=false; %高版MATLAB
%% BP神经网络初始权值和阈值
w1num=inputnum*hiddennum; % 输入层到隐层的权值个数
w2num=outputnum*hiddennum;% 隐层到输出层的权值个数
w1=x(1:w1num); %初始输入层到隐层的权值
B1=x(w1num+1:w1num+hiddennum); %初始隐层阈值
w2=x(w1num+hiddennum+1:w1num+hiddennum+w2num); %初始隐层到输出层的阈值
B2=x(w1num+hiddennum+w2num+1:w1num+hiddennum+w2num+outputnum); %输出层阈值
net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=reshape(B2,outputnum,1);
%% 训练网络以
net=train(net,P,T);
%% 测试网络
Y=sim(net,P_test);
err=norm(Y-T_test);
clc
clear all
close all
%% 加载神经网络的训练样本 测试样本每列一个样本 输入P 输出T
%样本数据就是前面问题描述中列出的数据
load data
% 初始隐层神经元个数
hiddennum=31;
% 输入向量的最大值和最小值
threshold=[0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1];
inputnum=size(P,1); % 输入层神经元个数
outputnum=size(T,1); % 输出层神经元个数
w1num=inputnum*hiddennum; % 输入层到隐层的权值个数
w2num=outputnum*hiddennum;% 隐层到输出层的权值个数
N=w1num+hiddennum+w2num+outputnum; %待优化的变量的个数
%% 定义遗传算法参数
NIND=40; %个体数目
MAXGEN=50; %最大遗传代数
PRECI=10; %变量的二进制位数
GGAP=0.95; %代沟
px=0.7; %交叉概率
pm=0.01; %变异概率
trace=zeros(N+1,MAXGEN); %寻优结果的初始值
FieldD=[repmat(PRECI,1,N);repmat([-0.5;0.5],1,N);repmat([1;0;1;1],1,N)]; %区域描述器
Chrom=crtbp(NIND,PRECI*N); %初始种群
%% 优化
gen=0; %代计数器
X=bs2rv(Chrom,FieldD); %计算初始种群的十进制转换
ObjV=Objfun(X,P,T,hiddennum,P_test,T_test); %计算目标函数值
while gen<MAXGEN
fprintf(‘%d\n‘,gen)
FitnV=ranking(ObjV); %分配适应度值
SelCh=select(‘sus‘,Chrom,FitnV,GGAP); %选择
SelCh=recombin(‘xovsp‘,SelCh,px); %重组
SelCh=mut(SelCh,pm); %变异
X=bs2rv(SelCh,FieldD); %子代个体的十进制转换
ObjVSel=Objfun(X,P,T,hiddennum,P_test,T_test); %计算子代的目标函数值
[Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代,得到新种群
X=bs2rv(Chrom,FieldD);
gen=gen+1; %代计数器增加
%获取每代的最优解及其序号,Y为最优解,I为个体的序号
[Y,I]=min(ObjV);
trace(1:N,gen)=X(I,:); %记下每代的最优值
trace(end,gen)=Y; %记下每代的最优值
end
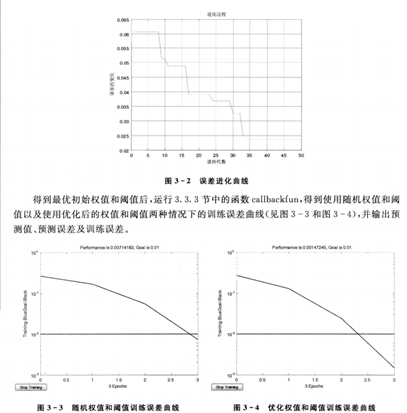
%% 画进化图
figure(1);
plot(1:MAXGEN,trace(end,:));
grid on
xlabel(‘遗传代数‘)
ylabel(‘误差的变化‘)
title(‘进化过程‘)
bestX=trace(1:end-1,end);
bestErr=trace(end,end);
fprintf([‘最优初始权值和阈值:\nX=‘,num2str(bestX‘),‘\n最小误差err=‘,num2str(bestErr),‘\n‘])
%% 比较优化前后的训练&测试
callbackfun
clc
%% 不适用遗传算法
%% 使用随机权值和阈值
inputnum=size(P,1); % 输入层神经元个数
outputnum=size(T,1); % 输出层神经元个数
%% 新建BP网络
net=newff(minmax(P),[hiddennum,outputnum],{‘tansig‘,‘logsig‘},‘trainlm‘);
%% 设置网络参数:训练次数为1000,训练目标为0.01,学习速率为0.1
net.trainParam.epochs=1000;
net.trainParam.goal=0.01;
LP.lr=0.1;
%% 训练网络以
net=train(net,P,T);
%% 测试网络
disp([‘1、使用随机权值和阈值 ‘])
disp(‘测试样本预测结果:‘)
Y1=sim(net,P_test)
err1=norm(Y1-T_test); %测试样本的仿真误差
err11=norm(sim(net,P)-T); %训练样本的仿真误差
disp([‘测试样本的仿真误差:‘,num2str(err1)])
disp([‘训练样本的仿真误差:‘,num2str(err11)])
%% 使用遗传算法
%% 使用优化后的权值和阈值
inputnum=size(P,1); % 输入层神经元个数
outputnum=size(T,1); % 输出层神经元个数
%% 新建BP网络
net=newff(minmax(P),[hiddennum,outputnum],{‘tansig‘,‘logsig‘},‘trainlm‘);
%% 设置网络参数:训练次数为1000,训练目标为0.01,学习速率为0.1
net.trainParam.epochs=1000;
net.trainParam.goal=0.01;
LP.lr=0.1;
%% BP神经网络初始权值和阈值
w1num=inputnum*hiddennum; % 输入层到隐层的权值个数
w2num=outputnum*hiddennum;% 隐层到输出层的权值个数
w1=bestX(1:w1num); %初始输入层到隐层的权值
B1=bestX(w1num+1:w1num+hiddennum); %初始隐层阈值
w2=bestX(w1num+hiddennum+1:w1num+hiddennum+w2num); %初始隐层到输出层的阈值
B2=bestX(w1num+hiddennum+w2num+1:w1num+hiddennum+w2num+outputnum); %输出层阈值
net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=reshape(B2,outputnum,1);
%% 训练网络以
net=train(net,P,T);
%% 测试网络
disp([‘2、使用优化后的权值和阈值‘])
disp(‘测试样本预测结果:‘)
Y2=sim(net,P_test)
err2=norm(Y2-T_test);
err21=norm(sim(net,P)-T);
disp([‘测试样本的仿真误差:‘,num2str(err2)])
disp([‘训练样本的仿真误差:‘,num2str(err21)])
function Obj=Objfun(X,P,T,hiddennum,P_test,T_test)
%% 用来分别求解种群中各个个体的目标值
%% 输入
% X:所有个体的初始权值和阈值
% P:训练样本输入
% T:训练样本输出
% hiddennum:隐含层神经元数
% P_test:测试样本输入
% T_test:测试样本期望输出
%% 输出
% Obj:所有个体的预测样本的预测误差的范数
[M,N]=size(X);
Obj=zeros(M,1);
for i=1:M
Obj(i)=Bpfun(X(i,:),P,T,hiddennum,P_test,T_test);
end


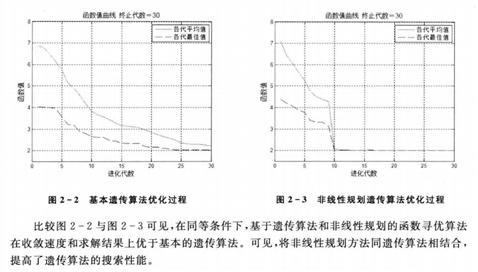
遗传算法可以解决我们的非线性规划问题,也可以优化BP神经网络,使神经网络预测的更加准确。
下次我们介绍粒子群算法解决非线性规划问题以及TSP问题和MTSP问题。
原文:https://www.cnblogs.com/Cassiopeia/p/15115459.html