最小生成树的概念

prim算法以及kruskal算法，原生问题中是求解将n个节点连接并花费最小而形成的树的算法。还可以求解最大的边权最小的问题。

相关题目后续补充

求最小生成树的算法

Prim算法

总是链接离中心最近的一个节点到树中。

O(n ^ 2)

原理解释：

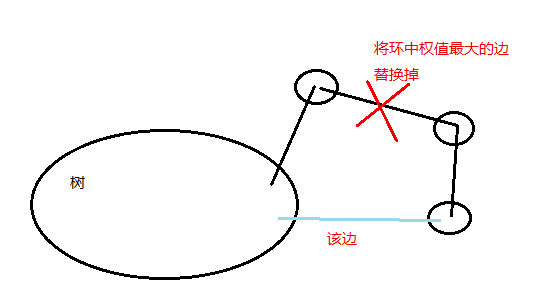
1. 反证法：将当前与外界直接相连的权值最小的一条边不并入树中，而是通过其他点将两个连通块连接构成了一棵树。在树构成完成之后，将该边并入树中，根据树的性质可以得到一个环，由于一开始两个连通块并不连通，一定是通过一条比该边权值更大的边进行连通的，所以该环一定会出现比该边权值更大的边，于是可以将环中权值最大的边去掉，仍然可以得到一棵树并且整棵树权值不会减小，于是得证该边一定可以并入该最小生成树中。

   

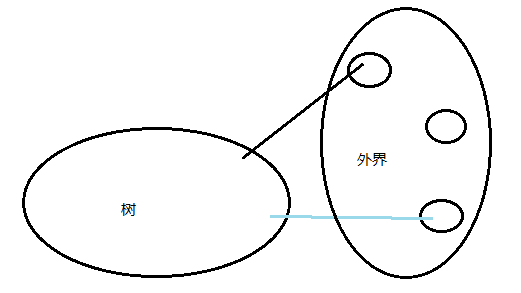
2. 连通性：将树与外界分开，将外界所有节点视为已经连通的连通块，如果最后要构成一棵树的话，显然需要一条边将“树”和“外界”进行连通。那么最优解显然就是权值最小的那一条边。

   

kruskal算法

类似于Bellman-Ford算法，去中心化，最终得到一棵树。直接存储边的结构体实现。

O(ElogE)，如果不用排序可以优化到O(E)

原理解释：

1. 反证法：和prim算法的证明差不多，大致环节就是，如果不加该边→成树→加上该边得到环→替换掉一条权值更大的边→更优解→该边可以出现在最后的最小生成树中。
2. 最优解：总是将权值最小的边并入树中，如果成环了，那么由于已经并入的都是比该边权值更小的边，所以环上一定不存在可替换的边，将该边舍去，如果不会成环，那就将其视为可以作为最小生成树的一条边。

特点：

计算中的任意过程拿出来都是正确的，可以中途结束，同样可以中途开始。是一个逐渐连接各个连通块，逐渐减少连通块个数的方法，因此可以可以求解类似最小生成森林的问题。

关键词：连通块，最小边。

拓展应用

1. 虚拟原点：可以完成点权转换为边权，将一些特殊的东西一般化。
2. 最小边：Kurskal算法的灵活应用需要关注算法过程中的连通块和最小边，这是一个很重要的性质。
3. 次小生成树：最小生成树的一类问题，最小生成树的邻集。

次小生成树

定义：第二小的生成树，不严格的话可以等于最小生成树，严格的话一定小于最小生成树。

求解方法：

1. 先求最小生成树，枚举删去最小生成树中的边求解。O(mlogm + m)
2. 先求最小生成树，枚举非树边，将该边加入树中，替换掉环上刚好比该边小(根据性质，一定是环上权值最大)的一条边。O(m + n^2 + mlogm)，如果使用LCA倍增优化，可以达到O(mlogm)

算法专题——最小生成树

原文：https://www.cnblogs.com/TanJI-life/p/15125807.html