拓扑排序 （DFS和BFS及判断是否有环）

一、什么是拓扑排序？

在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

• 每个顶点出现且只出现一次。
• 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

拓扑排序其实还是挺奇妙的，就是解决谁先谁后的问题

例如，下面这个图：

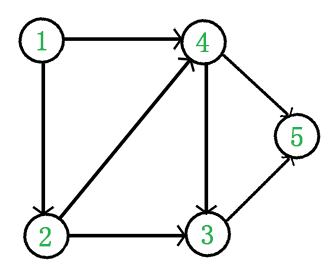
1. 从 DAG 图中选择一个没有前驱（即入度为0）的顶点并输出。

2. 从图中删除该顶点和所有以它为起点的有向边。

3. 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。

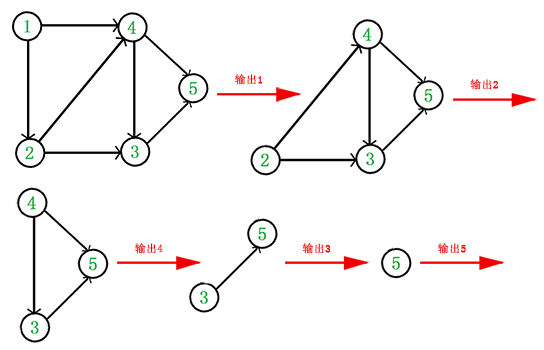
通常，一个有向无环图可以有一个或多个拓扑排序序列。这是因为可能同时存在多个入度为0的结点，这时，先处理哪个都是可以的。

二. 拓扑排序用来干什么？

• 判断是否有环
• 求DAG中的最长链

拓扑排序有两种方式，就是bfs和dfs,一般书中介绍的大多数是bfs,大家就以为拓扑排序只有一种办法，其实是不对的。

参考链接 ：https://blog.csdn.net/weixin_43918531/article/details/86740991

三、拓扑排序的bfs模板

有一个明确的思路：每一个顶点都有入度和出度，入度为0说明没有指向他的，那么就从他开始往下找。把这个入度为0的push进队列（还要注意保存入度为0的点），同时把与这个点相连的所有点的入度-1，然后再看看有没有入度为0的，有的话继续push，循环上面的操作，直到没有入度为0的点。
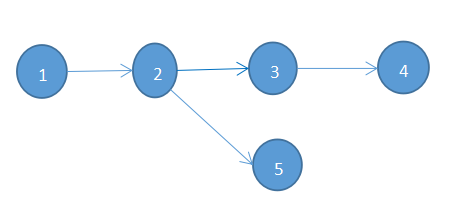
看一下上面的图，如果从序号1开始的话：1入度为0，push进队列，顶点2的入度-1，所以顶点2push进队列，3和5的入度-1，3push进队列，5push进队列，顶点3进队列后，顶点4入度-1,顶点4push进队列，所以输出结果就是1 2 3 5 4

#include <bits/stdc++.h>

using namespace std;
const int INF = 0x3f3f3f3f;


//本代码功能：以bfs输出一个有向无环图DAG的拓扑序
const int N = 1010;
vector<int> edge[N];    //邻接表
int ind[N];             //入度数组
queue<int> q;          //队列

int n;          //n个结点
int m;          //m条边
int main() {
    //读入，建图
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        edge[x].push_back(y);
        ind[y]++;//维护入度
    }
    //入度为零的放入队列
    for (int i = 1; i <= n; i++) if (!ind[i]) q.push(i);

    //广度优先搜索DAG，就是拓扑排序的模板
    while (!q.empty()) {
        int x = q.front();
        q.pop();
        //输出拓扑序
        cout << x << " ";
        for (int i = 0; i < edge[x].size(); i++) { //遍历所有出边
            int y = edge[x][i];                    //目标结点
            //对接点入度-1，抹去这条入边
            ind[y]--;
            //如果入度为0，则入队列，准备处理它
            if (!ind[y]) q.push(y);
        }
    }
    return 0;
}
/**
测试数据
 5 4

 1 2
 2 3
 2 5
 3 4

参考答案：
1 2 5 3 4
 */

四、拓扑排序的dfs模板

DFS是从一个点不断往下递归，比如说从序号1往下递归，有箭头就一直往下进行，直到到了最后一个元素，就开始往栈里（当然也可以是vector之类的，只不过需要反向再输出）push元素。比如说上面的从序号1开始，到序号2，序号3，序号4，到尽头了，就把4push进栈中，3push进栈，这个时候由于5也是2的下一个元素，所以5push进栈中，2push进栈，1push进栈，然后输出就是1 2 5 3 4.
当然这个递归的顺序是与你输入的顺序有关的，不过思路都是这样的，由起始点向下递归。

#include <bits/stdc++.h>

using namespace std;
const int INF = 0x3f3f3f3f;

//本代码功能：以dfs输出一个有向无环图DAG的拓扑序
const int N = 1010;

bool st[N];             //标识是不是已经使用过
vector<int> edge[N];    //邻接表
vector<int> res;        //拓扑序列

/**
 * 功能：深度优先搜索，记录拓扑序
 * @param u
 */
void dfs(int u) {
    //如果访问过了，则返回，不再重复访问
    if (st[u])return;
    //标识u结点已使用
    st[u] = true;

    //遍历每个出边,找到下一组结点
    for (int v:edge[u]) if (!st[v]) dfs(v);

    //这一层完毕才把它自己扔进去,最后扔等于最先输出，因为后面是倒序输出的
    res.push_back(u);
}

int n;          //n个结点
int m;          //m条边
int main() {
    //读入，建图
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        edge[x].push_back(y);
    }
    //将所有结点进行深入优先搜索
    for (int i = 1; i <= n; i++) dfs(i);

    //输出，从后向前输出
    for (int i = res.size() - 1; i >= 0; i--)
        cout << res[i] << " ";
}

/**
测试数据
 5 4

 1 2
 2 3
 2 5
 3 4

参考答案：
1 2 5 3 4
 */

拓扑排序 （DFS和BFS及判断是否有环）

原文：https://www.cnblogs.com/littlehb/p/15125824.html