题目

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node‘s key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node‘s key.
  Both the left and right subtrees must also be binary search trees.
• A Complete Binary Tree (CBT) is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.

Now given a sequence of distinct non-negative integer keys, a unique BST can be constructed if it is required that the tree must also be a CBT. You are supposed to output the level order traversal sequence of this BST.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤1000). Then N distinct non-negative integer keys are given in the next line. All the numbers in a line are separated by a space and are no greater than 2000.

Output Specification:

For each test case, print in one line the level order traversal sequence of the corresponding complete binary search tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.

Sample Input:

10
1 2 3 4 5 6 7 8 9 0
结尾无空行

Sample Output:

6 3 8 1 5 7 9 0 2 4
结尾无空行

解析

本来想的是先按题目顺序建树，然后按照完全二叉树改造树，再按层序输出，卡在改造二叉树上了，没能利用上完全二叉树的条件“当前节点序号俄日i，左孩子序号为2i，右孩子序号为2i+1”。
参考别人的算法：BST的中序遍历是按照从小到大的顺序的，而完全二叉树知道节点后可确定树，按照顺序排列好数组后，按中序遍历的顺序，给完全二叉树的数组赋值。

所以代码中树的操作都白扯了……看个乐吧。

Code

#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
int BST[1001], CBST[1001];
int BST_index = 0;  //用于更新根节点（数组）值
typedef struct tnode {
    /*树节点*/
    int data;
    struct tnode *lchild, *rchild;

} Tnode, *Tree;
typedef struct qnode {
    /*队列节点*/
    Tnode* pNode;
    struct qnode* next;
} Qnode;
typedef struct {
    /*队列结构*/
    Qnode *front, *rear;
} * Queue;

/********函数声明********/
Tree buildTree(int N);
Tree newNode(int data);
Tree insert(Tree T, int data);
void freeTree(Tree T);

void levelOrder(Tree T);
Queue initQueue();
bool isEmpty(Queue Q);
bool enQueue(Queue Q, Tnode* ptr);
bool deQueue(Queue Q, Tnode** ptr);

void adjustTree(int N);
void inOrder(int x, int N);

/*****主函数******/
int main() {
    int N;
    scanf("%d", &N);
    Tree T = buildTree(N);
    // levelOrder(T);

    /*调整成Complete BST*/
    adjustTree(N);
    freeTree(T);
    return 0;
}

/**********函数定义**********/
Tree buildTree(int N) {
    /*建立树*/
    int i, Data;
    /*创建根节点*/
    scanf("%d", &Data);
    BST[0] = Data;  //构建数组
    Tree T = newNode(Data);
    /*插入节点*/
    for (i = 1; i < N; i++) {
        scanf("%d", &Data);
        BST[i] = Data;  //构建数组
        insert(T, Data);
    }
    return T;
}
Tree newNode(int data) {
    /*建立新节点*/
    Tree T = (Tree)malloc(sizeof(Tnode));
    T->data = data;
    T->lchild = T->rchild = NULL;
    return T;
}
Tree insert(Tree T, int data) {
    /*按序插入子节点*/
    if (T == NULL)
        T = newNode(data);
    else if (data < T->data) {
        /*插入左子树*/
        T->lchild = insert(T->lchild, data);
    } else if (data > T->data) {
        /*插入右子树*/
        T->rchild = insert(T->rchild, data);
    }
    return T;
}
void freeTree(Tree T) {
    if (T->lchild)
        freeTree(T->lchild);
    if (T->rchild)
        freeTree(T->rchild);
    free(T);
}
void levelOrder(Tree T) {
    /*层序输出树T*/
    Queue S = initQueue();
    Tnode* index = (Tnode*)malloc(sizeof(Tnode));
    enQueue(S, T);
    while (!isEmpty(S)) {
        deQueue(S, &index);
        printf("%d", index->data);
        if (index->lchild)
            enQueue(S, index->lchild);
        if (index->rchild)
            enQueue(S, index->rchild);
        /*如果左右入队完成是空队，说明树已经输出完成*/
        if (!isEmpty(S))
            putchar(‘ ‘);
    }
}
Queue initQueue() {
    Queue Q = (Queue)malloc(sizeof(Qnode));
    Q->front = Q->rear = (Qnode*)malloc(sizeof(Qnode));
    Q->front->next = NULL;
    return Q;
}
bool isEmpty(Queue Q) {
    if (Q->rear == Q->front)
        return true;
    else
        return false;
}
bool enQueue(Queue Q, Tnode* ptr) {
    /*入队*/
    Qnode* p = (Qnode*)malloc(sizeof(Qnode));
    p->pNode = ptr;
    p->next = NULL;
    Q->rear->next = p;
    Q->rear = p;
    return true;
}
bool deQueue(Queue Q, Tnode** ptr) {
    /*出队*/
    if (isEmpty(Q))
        return false;
    Qnode* temp = Q->front->next;
    *ptr = temp->pNode;
    Q->front->next = temp->next;

    if (Q->rear == temp)
        Q->rear = Q->front;
    free(temp);
    return true;
}

void adjustTree(int N) {
    /*先排序*/
    int flag = 1;  //判断冒泡排序是否完成
    while (flag) {
        flag = 0;
        for (int i = 0; i < N - 1; i++) {
            if (BST[i] > BST[i + 1]) {
                flag = 1;
                int temp = BST[i];
                BST[i] = BST[i + 1];
                BST[i + 1] = temp;
            }
        }
    }

    int x = 1;
    inOrder(x, N);
    /*输出层序完全二叉树*/
    printf("%d", CBST[1]);
    for (int i = 2; i <= N; i++) {
        printf(" %d", CBST[i]);
    }
    return;
}
void inOrder(int x, int N) {
    if (x <= N) {
        //遍历左子树
        inOrder(x + x, N);
        //访问节点
        CBST[x] = BST[BST_index++];
        //遍历右子树
        inOrder(x + x + 1, N);
    }
}

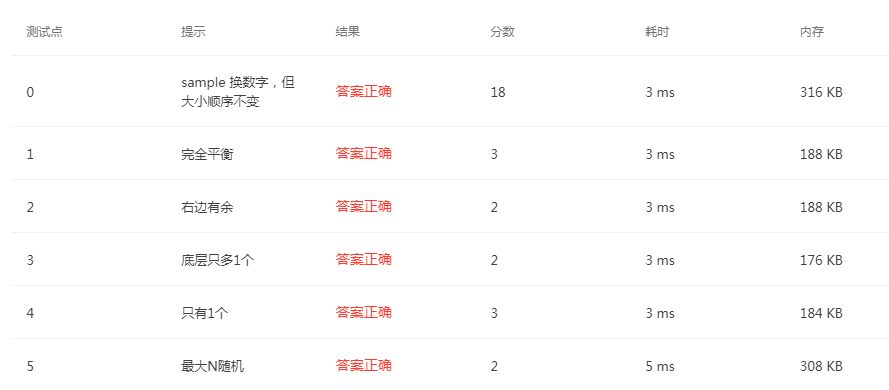
MOOC数据结构PTA-04-树6 Complete Binary Search Tree

原文：https://www.cnblogs.com/wundt-asim/p/15130593.html