直观地说,如果一个变换具有以下两条性质,我们就称它是线性的:
一是直线在变换后仍然保持为直线,不能有所弯曲(变换后对角线也必须是直线,也就是变换后的x轴和y轴保持平行且等分)
二是原点必须保持固定
总的来说,你应该吧线性变换看作是
保持网格平行且等距分布,并保持原点不动的变换
变换前如图:
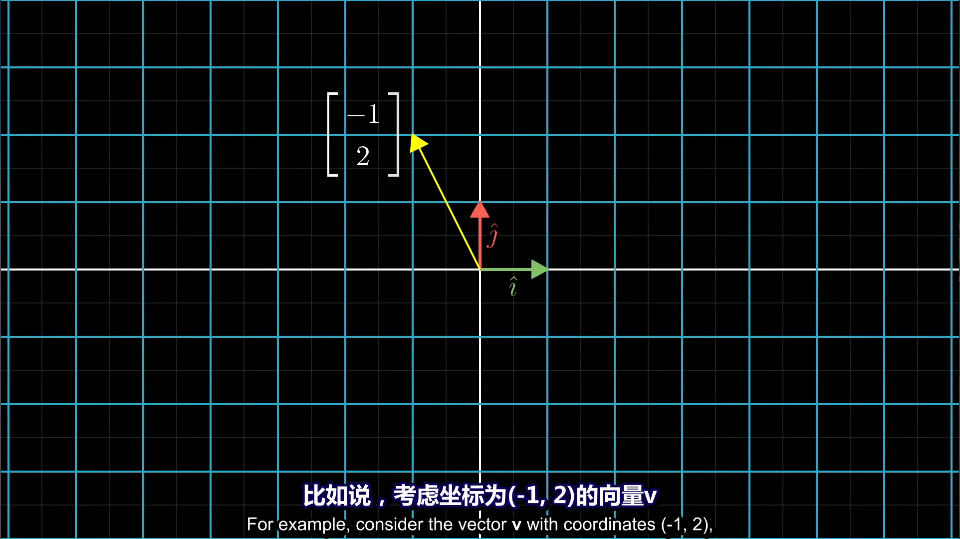
变换后如图:(网格线保持平行且等分的性质有一个重要的推论:变换后的向量v的位置,是-1与变换后的i帽之积,加上2与变换后的j帽之积)

变换后的向量v也是变换后的i帽和j帽的同样的线性组合:


我们只要记录了变换后的i帽和j帽,我们可以推断出任意向量在变换之后的位置,我们可以不用关心变换本身是什么

一个二维线性变换仅由四个数字完全确定,变换后i帽的两个坐标与变换后j帽的两个坐标
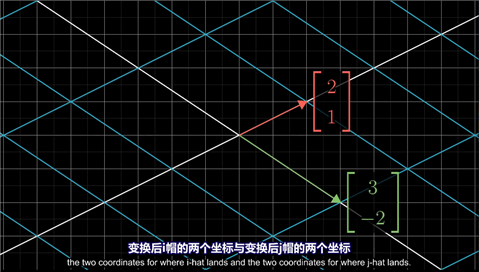
因此我们可以把一个2x2矩阵看做是两个特殊的向量,即变换后的i帽和j帽
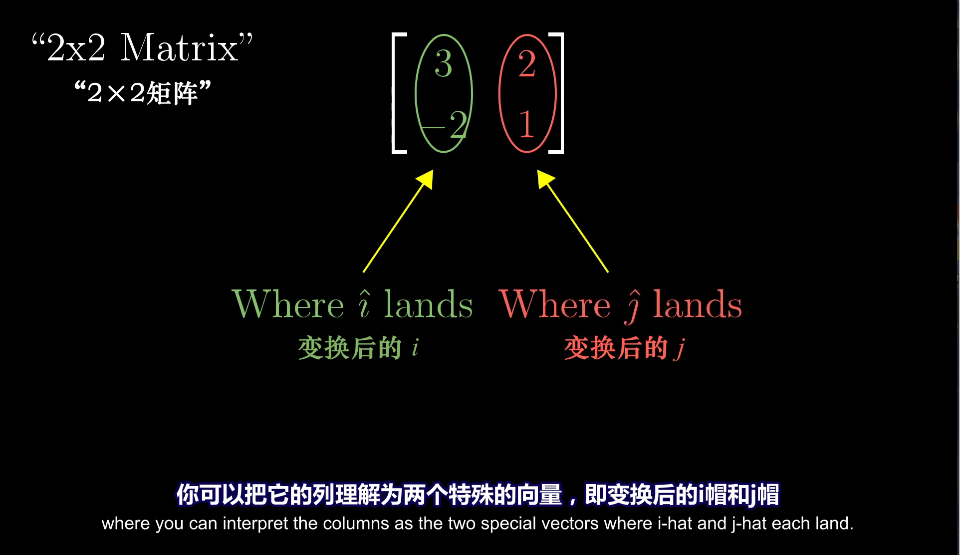
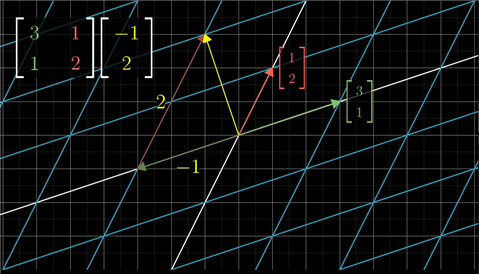
矩阵向量乘法:

每当看到一个矩阵,你都可以把它解读为对空间的一种特定变换:将矩阵看做空间的变换

我们完全可以把矩阵的列看做变换后的基向量,把矩阵向量乘法看做他们的线性组合
原文:https://www.cnblogs.com/hanshuai/p/15142402.html