| Data Structure | 数据结构 | Algorithm | 算法 |
|
Array |
数组 | General Coding | 一般编码 |
| Stack / Queue | 栈 / 队列 | In-order / Pre-order / Post-order traversal | 前序 / 中序 / 后序 遍历树 |
| PriorityQueue(heap) | 优先队列(堆) | Greedy | 贪心算法 |
| LinkedList(single / double) | 单向链表 / 双向链表 | Recursion / Backtrace | 递归 / 回溯 |
| Tree / Binary Tree | 树 / 二叉树 | Breadth-first search | 广度优先查找 |
| Binary Search Tree | 二分查找树 | Depth-first search | 深度优先查找 |
| HashTable | 散列表 | Divide and Conquer | 分词算法 |
| Disjoint Set | 并查集 | Dynamic Programming | 动态规划 |
| Trie | 字母树 | Binary Search | 二分查找 |
| BloomFilter | 布隆过滤器 | Graph | 图 |
| LRU Cache | 最近使用缓存 |
O(1) : Constant Complexity 常数复杂度
O(logn):Logarithmic Complexity 对数复杂度
O(n):Linear Complexity 线性时间复杂度
O(n^2):N square Complexity N的平方复杂度
O(n^3):N square Complexity N的立方复杂度
O(2^n):Exponential Growth 指数
O(n!):Factorial 阶乘
注意:多个复杂度进行联合算法,只看最高复杂度即可。
复杂度示例:
O(1)
int n = 1000;
System.out.print("hey boy" + n);
O(n)
for(int i = 1; i <= n; i ++) {
System.out.println(" hey boy, i am " + i);
}
O(n ^ 2)
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= n; j++) {
System.out.println(" hey boy, i am" + i + " and " + j);
}
}
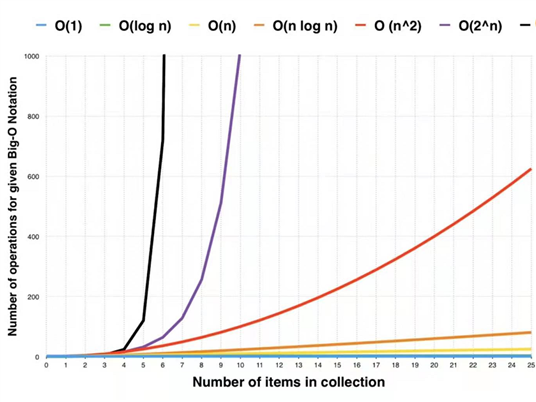
总结:由下图可以看出,不同时间复杂度随着时间的推移,差距会越来越大。所以当算法优化一点,在高并发情况下,收益会非常大。
To calculate
时间复杂度为O(n)
y = 0 for i = 1 to n: y = i + y
时间复杂度为O(1)
y = n * (n + 1) / 2
What a recursion ?
时间复杂度是O(2^n),代码虽然看起来很简单,但是计算机执行更复杂。
def fib(n):
if n == 0 or n == 1
return n
return fib(n - 1) + fib(n - 2)
主定律:Master Theorem
Application to common algorithms
| Algorithm | Recurrence relationship | Run time |
| Binary Search 二分查找 | T(n) = T(n/2) + O(1) | O(logn) |
| Binary tree traversal 二叉树遍历 | T(n) = 2T(n/2) + O(1) | O(n) |
| Optimal sorted matrix search 排序二维矩阵 | T(n) = 2T(n/2) + O(logn) | O(n) |
| Merge sort 快排,归并排序 | T(n) = 2T(n/2) + O(n) | O(n*logn) |
原文:https://www.cnblogs.com/yssd/p/15149828.html