AcWing 3808. 画正方形

原题链接

Description

现在，我们要在平面上画出 \(n\) 个边长为 1 的正方形。

注意，这 \(n\) 个正方形之间允许存在公共边。

每个正方形的所有端点坐标都必须为整数，且所有边都必须平行于坐标轴。

我们将逐边绘制整个图形。

当绘制某一条边时，如果该边的两端端点为 (\(x\),\(y\)) 和 (\(x\),\(y\)+1)，而我们在之前已经绘制了一条端点为 (\(x‘\), \(y\)) 和 (\(x‘\), \(y\)+1) 的边，则该边可以利用之前绘制的边作为参考，迅速画出。

同样的，如果即将绘制的边的两端端点为 (\(x\), \(y\)) 和 (\(x\)+1, \(y\))，而我们在之前已经绘制了一条端点为 (\(x\), \(y‘\)) 和 (\(x\)+1,\(y‘\)) 的边，则该边也可以利用之前绘制的边作为参考，迅速画出。

但是，如果即将绘制的边不满足上述条件，也就是不具备参考边，则为了保证绘图精确，我们需要借助尺子来绘制该条边。

例如，当 \(n=1\) 时，我们首先需要借助尺子绘制两条边，如下：

然后，借助以上两边完成剩余两边的绘制：

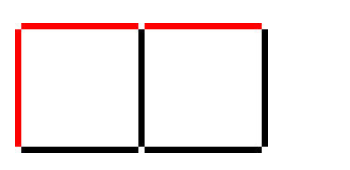
当 \(n=2\) 时，我们首先需要借助尺子绘制三条边，如下：

然后，借助以上三边完成剩余所有边的绘制：

我们希望在画出 \(n\) 个边长为 1 的小正方形的同时，借助尺子绘制的边的数量尽可能少。

请问，最少需要用尺子画多少条边。

Input

第一行包含整数 \(T\)，表示共有 \(T\) 组测试数据。

每组数据占一行，包含一个整数 \(n\)。

Output

每组数据输出一行结果，表示需要用尺子绘制的最少边数。

Solution

使用最少的尺子，就是所需要行和列最少数， 也就是上图中红色部分最少数，设\(y\)为上行的数量，\(x\)为左列的数量，正方形数量\(z\)，要是\(x\) + \(y\) 最小， 很明显当 \(x\) 和 \(y\) 接近的时候最小（重要不等式 \(a+b>2\sqrt{ab}\),当\(a==b\)时候取等号）, 所以 \(x=\sqrt{z},y=\lfloor \frac{z}{x} \rfloor\) 如果 \(x*y==z\)，就直接返回\(x+y\),否则，说明还有余数，需要再使用一次尺子，则返回\(x+y+1\)

Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

int work(int n)
{
    int x = sqrt(n);
    int y = n / x;
    int r = n % x;
    if(r)
        return x + y + 1;
    else
        return x + y;
}
int main()
{
    int T;
    cin >> T;
    
    while (T --)
    {
        int n;
        cin >> n;
        
        cout << work(n) << endl;
    }
}

AcWing 3808. 画正方形

原文：https://www.cnblogs.com/CharlesLC/p/15158523.html