图(graph)
一、图的定义
用顶点、边构成的存储结构。有:
G=(V,E)(graph=(Vertex,Edge))
Vertex就是顶点的有穷非空集合,Edge就是边的的 有穷集合。
二、图的术语
- 有向图/无向图:无向图中的边叫边,有向图中的边叫弧
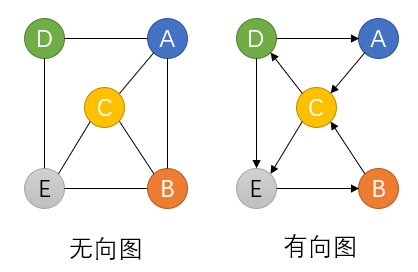
- 完全图:对无向图取任意两个顶点都有一条边相连,n(n-1)/2条;对有向图取任意两个顶点都有两条不同方向的弧,n(n-1)条。
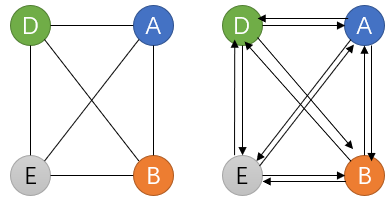
- 稀疏图:有很少边或弧的图。(个数<nlog2n)
- 稠密图:有较多或弧的图
- 网:边/弧带权的图
- 邻接:两个顶点的关系,无向图中称A与B互为邻接;有向图中称A邻接到B,B邻接于A。
- 关联:边/弧与顶点之间的关系。一条边/弧连接两顶点,则称该边/弧关联于这两个顶点
- 顶点的度:与该顶点相关联的边/弧数目。有向图中,顶点的度等于入度和出度之和。
- 路径:接续的边构成的顶点序列
- 路径长度:路径上边/弧的数目/权值之和。
- 回路(环):第一个顶点和最后一个顶点相同的路径
- 简单路径:各顶点均不相同的路径。
- 简单回路:除起点顶点,其余顶点均不相同的回路。
- 连通图:任意两顶点都有路径的图。有向图中连通图称为强连通图。
- 子图:如下
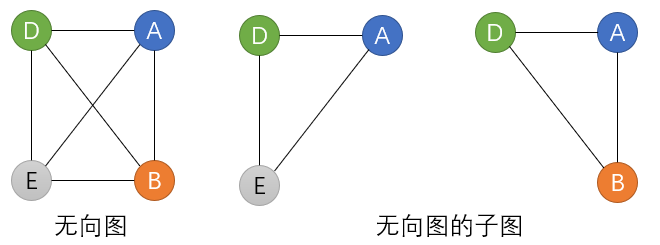
- 极大连通子图:该子图是G连通子图,将G的任何不在该子图的顶点加入,子图不再连通。
- (强)连通分量:图的极大连通子图。
- 极小连通子图:该子图是G连通子图,将该子图中删除任何一条边,子图不再连通。
三、图的类型和基本操作
数据基本类型加关系。
重要的基本操作:
初始条件:V是图的顶点集,VR是图中弧的集合
操作结果:按V和VR的定义构造图G
初始条件:图G存在
操作结果:对图进行深度优先遍历
初始条件:图G存在
操作结果:对图进行广度优先遍历
数据结构之图
原文:https://www.cnblogs.com/Pangenda/p/15170447.html


