Leetcode - 51. N 皇后

n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数n，返回所有不同的n皇后问题的解决方案。
每一种解法包含一个不同的n皇后问题的棋子放置方案，该方案中 ‘Q‘ 和 ‘.‘ 分别代表了皇后和空位。

示例 1：

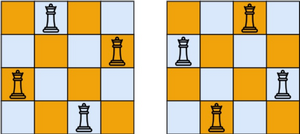
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9
• 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/n-queens
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

（未完成）解1 2021/9/7 O(?)

def solveNQueens(n: int) -> list:
    ‘‘‘
    .Q..
    ...Q
    Q...
    ..Q.

    ..Q.
    Q...
    ...Q
    .Q..
    ‘‘‘
    ‘‘‘
    一个一个放？
    比如，（x表示不能放了）
    q   x   x   x
    x   x   .   .
    x   .   x   .
    x   .   .   x
    
    q   x   x   x
    x   x   q   x
    x   x   x   x
    x   .   x   x
    只剩1个空位了，不行
    
    不过这个遍历的深度不小，O(n^2)后面一层一层下去
    试试吧
    ‘‘‘
    # 棋盘
    qipan=[[‘.‘]*n]*n
    # 剩余的Q
    remain_q=n
    # 剩下的空位，存位置(x,y)
    blank=[]
    for x in range(0,n):
        for y in range(0,n):
            qipan[x][y]=‘Q‘
            remain_q-=1
            # 初始化blank
            for i in range(0,n):
                for j in range(0,n):
                    # 横，竖
                    if i==x or j==y: continue
                    # 斜，斜就是斜率，±1
                    if abs((j-y)/(i-x))==1: continue
                    blank.append((i,j))
            # 开始填剩下的Q
            while remain_q and blank.__len__():
                # 貌似又要递归，写不下去了
    pass

if __name__ == ‘__main__‘:
    # [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
    n = 4
    # [["Q"]]
    n = 1

Leetcode - 51. N 皇后

原文：https://www.cnblogs.com/Code2235/p/15239821.html