Jordan Lecture Note-8: The Sequential Minimal Optimization Algorithm (SMO).

本文主要介绍用于解决SVM对偶模型的算法，它于1998年由John Platt在论文“Sequential Minimal Optimization:A Fast Algorithm for Training Support Vector Machines”中提出的。这篇笔记还参考了某篇博客，但由于是一年前的事了，暂时没找到这篇博客，所以没有引用出来，希望该篇博客的主人见谅。

（1）解决的问题。

    SMO 算法解决的是 soft SVM 对偶问题。其模型为：

 \begin{align}\mathop{\max}_{\alpha}&\quad W(\alpha)=\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j=1}^ny_iy_j\alpha_i\alpha_j\langle x_i,x_j\rangle\nonumber\\\mathop{s.t.}&\quad 0\leq\alpha_i\leq C\nonumber\\&\quad\sum_{i=1}^n\alpha_iy_i=0\label{model:SoftSVMDual}\end{align}

不失一般性，可以将$\langle x_i,y_j\rangle$替换为核函数，记为$K_{ij}$。对应的KKT条件为：

1. $\alpha_i=0\Longrightarrow y_i[x_i^\prime w+b]\geq 1$.
2. $\alpha_i=C\Longrightarrow y_i[x_i^\prime w+b]\leq 1$.
3. $0<\alpha_i<C\Longrightarrow y_i[x_i^\prime w+b]=1$.
   

（2）思路。

    对模型\ref{model:SoftSVMDual}（二次规划问题，QP），如果采用 interior point methods (比如 the projected conjugate gradient algorithm)的话，当训练集的数据量很大时，将产生一个非常大的矩阵，这对内存的要求以及效率影响非常大。SMO的思路就是把大的QP问题分解成一系列小的QP问题。具体点就是将向量$\alpha=(\alpha_1,\alpha_2,\cdots,\alpha_n)$中的大部分均固定住，只取其中的两个分量为变量，然后求解模型\ref{model:SoftSVMDual}。 其主要步骤如下：

repeat till convergence{ 

1. 采用启发式的方法选取一对$\alpha_i,\alpha_j$，然后固定其他分量；
2. 在$\alpha_i,\alpha_j$为变量的情况下求解模型\ref{model:SoftSVMDual}，更新$\alpha_i,\alpha_j$。

}

（3）SMO分析。

     不失一般性，我们假设选取的点为$\alpha_1,\alpha_2$，由限制条件$\sum_{i=1}^n\alpha_iy_i=0$可知$y_1\alpha_1+y_2\alpha_2=-\sum_{i=3}^n\alpha_iy_i\triangleq k$，其中$k$为常数。又由限制条件$0\leq\alpha_i\leq C$可知，可行解被限制在如下的两个盒子里。

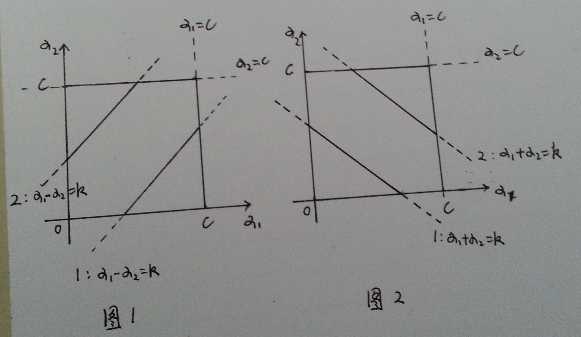
 对第二个限制条件$y_1\alpha_1+y_2\alpha_2=k$进行讨论。

1）当$y_1\neq y_2$时，$\alpha_1-\alpha_2=k$。设$\alpha_2$的上下界为$L,H$。

    若$k\geq 0$，则$\alpha_1,\alpha_2$只能在图1中直线一的实线部分，则此时$L=0,H=C-k$;

    若$k< 0$，则$\alpha_1,\alpha_2$只能在图1中直线二的实线部分，则此时$L=-k,H=C$;

2) 当$y_1=y_2$时，$\alpha_1+\alpha_2=k$。

    若$0\leq k\leq C$，则$\alpha_1,\alpha_2$只能在图2中直线一的实线部分，则此时$L=0,H=k$;

    若$k>C$，则$\alpha_1,\alpha_2$只能在图2中直线二的实线部分，则此时$L=k-C,H=C$。

综上，$\alpha_2$的取值范围为: $L\leq\alpha_2\leq H$。

对目标函数进行转化：

\begin{align*}W(\alpha_2)&=\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^ny_iy_jK_{ij}\alpha_i\alpha_j\\&=\alpha_1+\alpha_2+\sum_{i=3}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n(\sum_{j=1}^2y_iy_jK_{ij}\alpha_i\alpha_j+\sum_{j=3}^ny_iy_jK_{ij}\alpha_i\alpha_j)\\&=\alpha_1+\alpha_2+\sum_{i=3}^n\alpha_i-\frac{1}{2}\sum_{i=1}^2(\sum_{j=1}^2y_iy_jK_{ij}\alpha_i\alpha_j+\sum_{j=3}^ny_iy_jK_{ij}\alpha_i\alpha_j)\\&\quad-\frac{1}{2}\sum_{i=3}^n(\sum_{j=1}^2y_iy_jK_{ij}\alpha_i\alpha_j+\sum_{j=3}^ny_iy_jK_{ij}\alpha_i\alpha_j)\\&=\alpha_1+\alpha_2+\sum_{i=3}^n\alpha_i-\frac{1}{2}\sum_{i=1}^2\sum_{j=1}^2y_iy_j\alpha_i\alpha_jK_{ij}-\sum_{i=1}^2\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK_{ij}-\frac{1}{2}\sum_{i=3}^n\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK_{ij}\\&=\alpha_1+\alpha_2-\frac{1}{2}\alpha_1^2K_{11}-\frac{1}{2}\alpha_2^2K_{22}-y_1y_2\alpha_1\alpha_2K_{12}-y_1\alpha_1\sum_{j=3}^ny_j\alpha_jK_{1j}-y_2\alpha_2\sum_{j=3}^ny_j\alpha_jK_{2j}\\&\quad +\sum_{i=3}^n\alpha_i-\frac{1}{2}\sum_{i=3}^n\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK_{ij}\\&=\alpha_1+\alpha_2-\frac{1}{2}K_{11}\alpha_1^2-\frac{1}{2}K_{22}\alpha_2-y_1y_2K_{12}\alpha_1\alpha_2-y_1\alpha_1v_1-y_2\alpha_2v_2+\text{Constant}\end{align*}

其中$v_1=\sum_{j=3}^ny_j\alpha_jK_{1j},v_2=\sum_{j=3}^ny_j\alpha_jK_{2j}$。

   由$\sum_{i=1}^ny_i\alpha_i=0\Longrightarrow \alpha_1y_1+\alpha_2y_2=k\Longrightarrow \alpha_1=r-s\alpha_2$，其中$r=ky_1$为常数，$s=y_1y_2$。 将$\alpha_1=r-s\alpha_2$代入上式得到：

\begin{align*}W(\alpha_2)=&r-s\alpha_2+\alpha_2-\frac{1}{2}K_{11}(r-s\alpha_2)^2-\frac{1}{2}K_{22}\alpha_2^2-sK_{12}\alpha_2(r-s\alpha_2)\\&\quad-y_1(r-s\alpha_2)v_1-y_2\alpha_2v_2+\text{Constant}\end{align*}

对$W(\alpha)$求导并令导数为0得：

 \begin{align*}\frac{dW(\alpha_2)}{d\alpha_2}=-s+1+sK_{11}(r-s\alpha_2)-K_{22}\alpha_2-srK_{12}+2K_{12}\alpha_2+y_1v_1s-y_2v_2=0\end{align*}

$$\Longrightarrow(K_{11}+K_{22}-2K_{12})\alpha_2=1-y_1y_2+y_1y_2r(K_{11}-K_{12})+y_2(v_1-v_2)$$

\begin{equation}\Longrightarrow\alpha_2=\frac{y_2[y_2-y_1+y_1r(K_{11}-K_{12})+v_1-v_2]}{K_{11}+K_{22}-2K_{12}}\label{equ:solutionOfAlpha2}\end{equation}

 将$v_1=\sum_{j=3}^ny_j\alpha_jK_{1j}, v_2=\sum_{j=3}^ny_j\alpha_jK_{2j}, r=\alpha_1+s\alpha_2=\alpha_1^{old}+s\alpha_2^{old}$ 代入式子\ref{equ:solutionOfAlpha2}得：

\begin{equation}\alpha_2^{new}=\frac{y_2[y_2-y_1+y_1(\alpha_1^{old}+s\alpha_2^{old})(K_{11}-K_{12})+\sum_{j=3}^ny_j\alpha_jK_{1j}-\sum_{i=3}^ny_i\alpha_iK_{2i}]}{K_{11}+K_{22}-2K_{12}}\label{equ:updateAlpha2}\end{equation}

记$f(x_i)=\sum_{j=1}^ny_j\alpha_jK_{ij}+b$，即$f(x_i)=w^\prime x_i+b$，故可得$v_1,v_2$:

\begin{equation}v_1=\sum_{j=3}^ny_j\alpha_jK_{1j}=f(x_1)-b-y_1\alpha_1K_{11}-y_2\alpha_2K_{12}=f(x_1)-b-y_1\alpha_1^{old}K_{11}-y_2\alpha_2^{old}K_{12}\label{equ:v1}\end{equation}

\begin{equation}v_2=\sum_{j=3}^ny_j\alpha_jK_{2j}=f(x_2)-b-y_1\alpha_1K_{21}-y_2\alpha_2K_{22}=f(x_2)-b-y_1\alpha_1^{old}K_{21}-y_2\alpha_2^{old}K_{22}\label{equ:v2}\end{equation}

将式子\ref{equ:v1}和\ref{equ:v2}代入式子\ref{equ:updateAlpha2}得：

\begin{align}\alpha_2^{new}&=\frac{y_2[y_2-y_1+y_1(\alpha_1^{old}+s\alpha_2^{old})(K_{11}-K_{12})+f(x_1)-f(x_2)\\-y_1\alpha_1^{old}K_{11}-y_2\alpha_2^{old}K_{12}+y_1\alpha_1^{old}+y_2\alpha_2^{old}K_{22}]}{K_{11}+K_{22}-2K_{12}}\nonumber\\&=\frac{y_2[y_2-y_1+y_1\alpha_1^{old}(K_{11}-K_{12})+y_2\alpha_2^{old}(K_{11}-K_{12})\\+y_1\alpha_1^{old}(K_{21}-K_{11})+y_2\alpha_2^{old}(K_{22}-K_{21})+f(x_1)-f(x_2)]}{K_{11}+K_{22}-2K_{12}}\nonumber\\&=\frac{y_2[y_2-y_1+y_2\alpha_2^{old}(K_{11}-K_{12}+K_{22}-K_{21})+f(x_1)-f(x_2)]}{K_{11}+K_{22}-K_{12}}\nonumber\\&=\alpha_2^{old}+\frac{y_2[(f(x_1)-y_1)-(f(x_2)-y_2)]}{K_{11}+K_{22}-2K_{12}}\nonumber\\&\triangleq\alpha_2^{old}+\frac{y_2(E_1-E_2)}{\eta}\label{equ:newUpdateAlpha2}\end{align}

 其中$E_i=f(x_i)-y_i$表示误差项，$\eta=K_{11}+K_{22}-2K_{12}=\|\Phi(x_1)-\Phi(x_2)\|^2$.（$\Phi$是原始空间向特征空间的映射，其中$\sqrt{\eta}$可以看成是一个度量两个样本的相似性距离）

    得到$\alpha_2^{old}$的更新式子后，由于$\alpha_2^{old}$也必须落入限制盒子里，故必须对$\alpha_2^{new}$进行限制，即：

\begin{equation}\alpha_2^{new.clipped}=\left\{\begin{array}&L\quad\quad\quad\alpha_2^{new}\leq L\\\alpha_2^{new}\quad\quad\quad L<\alpha_2^{new}<H\\H\quad\quad\quad\alpha_2^{new}\geq H\end{array}\right.\label{equ:clippedAlpha2}\end{equation}

又因为$\alpha_1^{old}=r-s\alpha_2^{old},\alpha_1^{new}=r-s\alpha_2^{new.clipped}$，消去$r$得到：

\begin{equation}\alpha_1^{new}=\alpha_1^{old}+s\alpha_2^{old}-s\alpha_2^{new.clipped}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new.clipped})\label{equ:updateAlpha1}\end{equation}

得到更新$\alpha_1$与$\alpha_2$的两个迭代式：

$\alpha_2^{new}=\alpha_2^{old}+\frac{y_2(E_1-E_2)}{\eta}$，进一步求得$\alpha_2^{new.clipped}$

$\alpha_1^{new}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new.clipped})$.

（4）停止条件。

 待续。。。。

Jordan Lecture Note-8: The Sequential Minimal Optimization Algorithm (SMO).

原文：http://www.cnblogs.com/boostable/p/sequential_minimal_optimization.html