Dreamoon loves summing up something for no reason. One day he obtains two integers a and boccasionally.
He wants to calculate the sum of all nice integers. Positive integer x is called nice if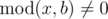 
and 
,
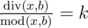where k is some integer number in range [1,?a].
By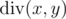 
we
denote the quotient of integer division of x and y.
By 
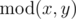we
denote theremainder of integer division of x and y.
You can read more about these operations here:http://goo.gl/AcsXhT.
The answer may be large, so please print its remainder modulo 1?000?000?007 (109?+?7). Can you compute it faster than Dreamoon?
The single line of the input contains two integers a, b (1?≤?a,?b?≤?107).
Print a single integer representing the answer modulo 1?000?000?007 (109?+?7).
1 1
0
2 2
8
For the first sample, there are no nice integers because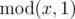 
is
always zero.
For the second sample, the set of nice integers is {3,?5}.
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
using namespace std;
const int MOD=1000000007;
int main()
{
long long a,b;
while(cin>>a>>b)
{
long long m=(1+b-1)*(b-1)/2%MOD;
//cout<<m<<endl;
long long sum=0;
{
for(long long i=1;i<=a;i++)
{
sum=(sum%MOD+m*((b*i)%MOD+1)%MOD)%MOD;
}
}
cout<<sum<<endl;
}
}Codeforces Round #272 (Div. 2) C
原文：http://blog.csdn.net/notdeep__acm/article/details/40051693