本文主要讲解在matlab中实现Linear Regression和Logistic Regression的代码,并不涉及公式推导。具体的计算公式和推导,相关的机器学习文章和视频一大堆,推荐看Andrew NG的公开课。
一、线性回归(Linear Regression)
方法一、利用公式 :
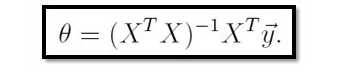
function [ theta ] = linearReg() %线性回归。 X=[1 1;1 2;1 3;1 4]; %注意第一列全为1,即x0=1,第二列才为x1 Y=[1.1;2.2;2.7;3.8]; A=inv(X‘*X); theta=A*X‘*Y; %根据公式theta=(X‘*X)^(-1)*X‘*Y; end
这种方法最简单,但是公式推导过程很复杂。
方法二:使用梯度下降法迭代
function theta=linearRegression() % 梯度下降法寻找最合适的theta,使得J最小 options=optimset(‘GradObj‘,‘on‘,‘MaxIter‘,100); inittheta=[1 1]‘; theta=fminunc(@costFunc,inittheta,options); end %% function [J,gradient]= costFunc(theta) %J为代价函数。 %y=theta(0)*x0+theta(1)*x1; 找出最好的theta来拟合曲线。 %使得J最小的theta就是最好的theta x=[1;2;3;4]; y=[1.1;2.2;2.7;3.8]; m=size(x,1); hypothesis=theta(1)+theta(2)*x; delta=hypothesis-y; J=sum(delta.^2)/(2*m); gradient(1)=sum(delta.*1)/m; %x0=1; gradient(2)=sum(delta.*x)/m; end
这两种方法,都采用数据:
x=[1;2;3;4];
y=[1.1;2.2;2.7;3.8];
当然,用的时候可以换成其它数据,两种方法得出的结果都是
theta =
0.3000
0.8600
即可以学习到线性函数:
Y=0.3000+0.8600*X;
二、Logistic回归(Logistic Regression)
方法一、利用matlab自带的函数glmfit() :
function theta=logisticRegression() % logistic regression的参数theta,可以用matlab自带函数glmfit求出 x = [0.0 0.1 0.7 1.0 1.1 1.3 1.4 1.7 2.1 2.2]‘; y = [0 0 1 0 0 0 1 1 1 1]‘; theta = glmfit(x, [y ones(10,1)], ‘binomial‘, ‘link‘, ‘logit‘) end
方法二:使用梯度下降法迭代
function theta =logisticReg() % 梯度下降法寻找最合适的theta,使得代价函数J最小 options=optimset(‘GradObj‘,‘on‘,‘MaxIter‘,100); inittheta=[0 0]‘; theta=fminunc(@costFunc,inittheta,options); end %% function [J,gradient] = costFunc(theta) x = [0.0 0.1 0.7 1.0 1.1 1.3 1.4 1.7 2.1 2.2]‘; y = [0 0 1 0 0 0 1 1 1 1]‘; m=size(x,1); tmp=theta(1)+theta(2)*x; %theta‘x hypothesis=1./(1+exp(-tmp)); %logistic function delta=log(hypothesis+0.01).*y+(1-y).*log(1-hypothesis+0.01); %加上0.01是为了防止x为0 J=-sum(delta)/m; gradient(1)=sum(hypothesis-y)/m; %x0=1; gradient(2)=sum((hypothesis-y).*x)/m; %theta=theta-a*gradient; gradient=-J‘(theta) end
两种方法都使用数据:
x = [0.0 0.1 0.7 1.0 1.1 1.3 1.4 1.7 2.1 2.2]‘;
y = [0 0 1 0 0 0 1 1 1 1]‘;
注意,Y的值只能取0和1两种。
得到结果:
theta =
-3.4932
2.9402
即可以学习到函数:
Y=1/(1+exp(3.4932-2.9402*x));
原文:http://www.cnblogs.com/denny402/p/4032381.html